算法小站
首页
wiki
新鲜事
文章搜索
网站导航
回忆录
首页
wiki
新鲜事
文章搜索
网站导航
回忆录
登录
注册
算法基础
搜索
数据结构
字符串
数学
图论
动态规划
计算几何
杂项
轮廓线动态规划
状态压缩dp中有一种很特殊的,解决棋盘类问题的工具,就是轮廓 .....
[[ slider_text ]]
[[ item.c ]]
0
0
轮廓线动态规划
发布时间
2024-09-12
作者:
秋千月
来源:
代码源
状态压缩dp
插头dp
轮廓线动态规划,是状压dp中非常特殊的一种类型,经常作为分析棋盘问题的工具 有的地方将其称为插头dp ## CCPC Qinghuangdao 2019 G **[CCPC Qinghuangdao 2019 G, Game on Chessboard](https://codeforces.com/gym/102361/problem/G)** **问题描述** 给定$$n \times n$$的棋盘,放了一些白子和黑子,每一个子有一个权值,你要玩消消乐 每一次可以选择一个子消除,代价是这个子的权值 也可以选择一个黑子和一个白子消除,代价是这两个子权值差的绝对值 消除有限制的,你要选择的子左下角没有别的棋子 问最后消除完所有棋子的最小代价 ### 算法分析 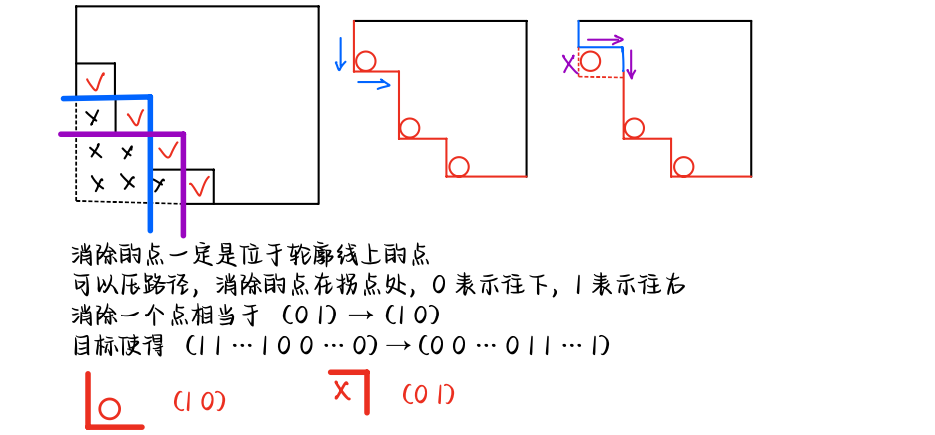 遍历相应的状态,$$S = (11\cdots 1 0 \cdots 0) \to (0 0 \cdots 011\cdots 1)$$ 把轮廓线上所有的元素,状压到$$S$$中 检查轮廓线上第$$i \in [0, 2n]$$个元素的状态,需要检查第$$i$$个元素的**最后 2 位** 我们需要检查$$(S \gg i) \textbf{ and } 3$$ 考虑沿着轮廓线,是怎么变化的 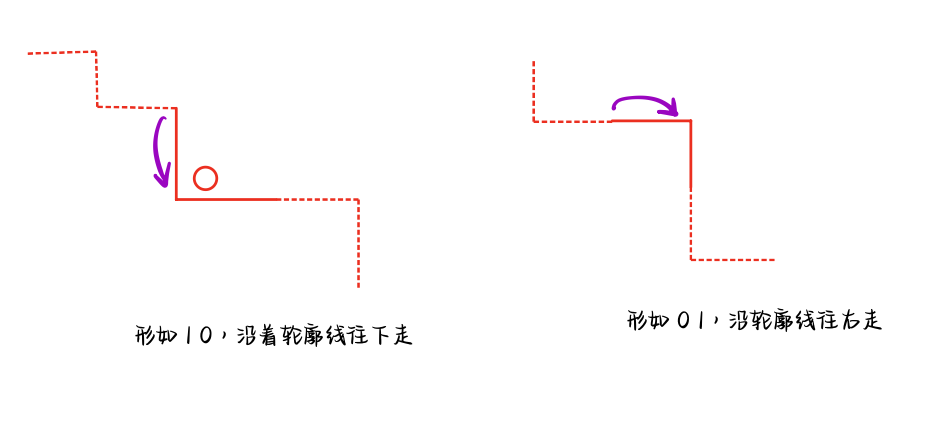 * 若$$(S \gg i) \textbf{ and } 3 = 2$$,那么形如$$(1 0)$$,说明$$i$$这个棋子位于轮廓线上 可以消去,另外,注意到还存在黑白棋同时消去的策略,还需要将这些棋子按照颜色分类,缓存起来 单独消去的策略,最后两位的状态变化$$(10) \to (01)$$,实际上需要$$\oplus 3$$,假设当前棋子在$$(x, y)$$ $$dp(S \oplus (3 \ll i)) \leftarrow dp(S) + cost(x, y)$$ 然后呢?**沿着轮廓线继续检查**,如果形如$$(10)$$,$$x \leftarrow x+1$$,形如$$(01)$$,$$y \leftarrow y+1$$ * 遍历走完轮廓线之后,对缓存下来的黑白棋,考虑黑白棋一起消掉的代价 不放设二元组$$(i1, w1), (i2, w2)$$分别表示黑白棋的编号和代价,存在转移 $$dp(S \oplus (3 \ll i1) \oplus (3 \ll i2)) \longleftarrow dp(S) + |w1 - w2|$$ ### 算法实现 ```bash int main() { vector<ll> dp(maxn, inf); dp[bit(2*n) - bit(n)] = 0; for (int S = bit(2*n) - 1; S >= 0; S--) if (dp[S] < inf) { // find a new line int x = 0, y = 0; int pb = 0, pw = 0; for (int i = 0; i < 2 * n; i++) { if ( ((S >> i) & 3) == 2) { chmin( dp[S ^ (3 << i)], dp[S] + 1LL * w[x][y] ); if (str[x][y] == 'B') bl[pb++] = {i, w[x][y]}; else wh[pw++] = {i, w[x][y]}; } if (S & bit(i)) y++; else x++; } for (int i = 0; i < pw; i++) for (int j = 0; j < pb; j++) { int i1 = wh[i].first, w1 = wh[i].second; int i2 = bl[j].first, w2 = bl[j].second; chmin(dp[S ^ (3<<i1) ^ (3<<i2)], dp[S] + abs(w1-w2)); } } ll ans = dp[ bit(n) - 1 ]; } ```
0
0
上一篇:状态压缩动态规划(二)
下一篇:计数动态规划
看完文章有啥想法
发布评论
494 人参与,0 条评论