wiki - 算法小站

wiki 主题

主题名称

是否为父主题

是否为其添加wiki文章

选择主题

修改主题名称

修改父主题

修改wiki文章

算法基础搜索数据结构字符串数学图论动态规划计算几何杂项

图论

图的连通性

有向图的强连通分量

无向图的割点割边和双连通分量

[[ item.c ]]

有向图强连通分量

##  DFS 森林和边
对于**有向图**的 DFS 森林，有几种重要的边，分别是 TreeEdge, BackEdge, FowardEdge, CrossEdge，大致如下
![](/media/content_img/tarjan-edges.jpeg)

有一些边比较重要，TreeEdge 是根据 dfs 的**时间戳**经过的边，BackEdge 为**返祖边**，
实际上就是指向之前祖先的边。（所谓祖先，就是时间戳较小的点，它们更早被访问到）

特别需要注意的是，CrossEdge，它是**横跨 dfs 分支**的边，并且它只能从**后访问的分支指向先访问的分支**，如红色所示。
> 可以用反证法，如果从$$(u, v)$$是 CrossEdge，但是$$v$$后访问的话，$$v$$就是$$u$$的儿子，矛盾

## 有向图的强连通分量

$$u, v$$强连通，指的是$$u, v$$两个点可以互相到达，强连通具有传递性

$$u, v$$强连通，$$v, w$$强连通，$$\Rightarrow \ u, w$$ 强连通

有向图的强连通分量 SCC，指的是把图划分成**极大的块**，使得块中的点两两强连通

## Tarjan 算法
### 算法思想

**引理**，SCC 一定是**dfs 树**中的连续的一块区域

> 证明如下，如上图所示，如果存在点$$c$$不在连通分量重，根据 SCC 的传递性
   必然存在从$$A \to B$$的往下路径，会经过$$C$$，即 $$A \to C, C \to B$$
   从而$$(A, B, C)$$属于同一个 SCC
   
>  那么，如果不经过$$C$$，即$$A, B$$在不同的分支中，但是他们又要连通，怎么办？
   要么是$$B \to A$$，通过 CrossEdge 相连
   要么是$$A \to B$$，$$A$$通过 BackEdge 返祖边连到某个**祖先**$$w$$，$$w$$再通过 TreeEdge 或者 ForwardEdge 连到后代$$B$$中
   
 **tarjan算法**，什么时候子树会形成一个 SCC 呢？
 根据引理，有以下条件
 
 * 子树中没有 BackEdge 连到祖先，子树块可能构成 SCC
 * 子树也可能通过 CrossEdge 连到之前的分支，通过**先前分支的** BackEdge 连到祖先
     如果这个条件也不满足，那么子树块就是一个 SCC
	 
Tarjan 算法的做法是，一边 dfs，一边**检查**，如果发现一个块已经是一个极大 SCC 了，就把它**切下来**

那么子树构成 SCC 的充要条件是
* 不能连到祖先去
* 不能通过 CrossEdge 连到前面**未被切下来**的点

概括地说，如果子树中有一个点可以**跳出子树区域**，那么子树不会被视为一个 SCC
跳不出子树，子树就形成一个 SCC

### 算法实现
需要维护三个值，分别是 $$dfn(u), low(u), ins(u)$$

*  `dfn(u)` 记录`u`的时间戳
*  `ins(u)` 记录`u`点有没有被**切掉**，怎么判断有没有被切呢？
    如果形成了极大`SCC`，那么切掉，否则的话，没有确定能形成`SCC`的点都把它放入栈中
	
*  `low(u)` 表示子树能往上跳到的`dfn`最小的点，并且跳的这个点$$v$$**未被切割**，即`ins(v) = True`
    概括地说，`low`判断子树能不能跳得出去
	
> 关于 `low(u)`的写法，在无向图中必须要严格一些，在有向图中有几种写法
   首先是，如果`(u, v)`是 TreeEdge，那么`low(u)`是一个树形`dp`的过程
   `low(u) = min(low(u), low(v))`
   否则`(u, v)`非树边，需要用`dfn`来更新，`low(u) = min(low(u), dfn(v))`
   
> 另一方面，在有向图中，实际上 `low(u)` 是辅助我们判断，子树能不能**跳出去**
   不必记录的那么精确
   ```bash
   edge (u, v):
       if (ins(v)):    low(u) = min(low(u), low(v))
   ```
   
>  如上所示也是可以的，只要看子树能不能跳出去就可以了

```bash
// bel[u] 来保存 u 属于哪一个连通分量
// scc 存连通分量的点
vector<int> bel(maxn, 0);
vector<vector<int> > scc;

stack<int> stk;
int idx = 0, cnt = 0;
function<void(int)> dfs = [&](int u) -> void {
	dfn[u] = low[u] = ++idx;
	stk.push(u);
	ins[u] = true;

for (auto v : G[u]) {
		if (!dfn[v]) dfs(v);
		if (ins[v]) low[u] = min(low[u], low[v]);
	}
	if (dfn[u] == low[u]) {
		vector<int> c;
		++cnt;
		while (true) {
			auto v = stk.top();
			stk.pop();
			c.push_back(v);
			ins[v] = false;
			bel[v] = cnt;
			if (v == u) break;
		}
		sort(c.begin(), c.end());
		scc.push_back(c);
	}
};
```

## HAOI 受欢迎的牛
**[受欢迎的牛](https://ac.nowcoder.com/acm/problem/19960)**
给定一个$$G(n, m)$$的图（表示$$n$$个点，$$m$$条边），$$(A \to B)$$关系具有传递性
$$(A \to B), (B \to C) \Longrightarrow (A \to C)$$
求有多少个点，使得所有的点都能够到达这些点

**算法分析**

*  如果图是一个`DAG`，那么这样的点只有一个，是唯一汇点
*  如果是一般图，`SCC`缩点之后，它是一个`DAG`，缩点之后的唯一汇点，均满足
   （SCC 内部的点不需要考虑，因为均可以互相到达）
   此时统计缩点之后的强连通分量，唯一汇点的`size`
*  多于`2`个汇点，直接返回`False`，因为均不可达

**算法实现**
怎么判断唯一汇点，可以考虑**缩点**，缩点之后看点的**出度**，`deg = 0`的那个缩点就是唯一汇点
注意的是，同一个强连通分量中，可能有边反复相连，我们只需要考虑**横跨不同连通分量的边**即可
即满足$$(u, v), \ bel_u \neq bel_v$$

##  最大半连通子图
**[ZJOI2007 最大半连通子图](https://ac.nowcoder.com/acm/problem/20603)**
**问题描述**，有向图称为半连通的，当它满足$$(u, v)$$，存在$$u \to v$$**或者**$$v \to u$$路径就可以
导出子图，指图中选一些点$$V' \in V$$，同时把$$V'$$关联的所有边$$E'$$也选了，那么构成的图是导出子图$$G'$$
如果$$G'$$半连通，称为$$G$$的半连通子图，这些子图中包含节点数最多的，称$$G'$$是$$G$$的最大半连通子图

给定有向图$$G$$，求出$$G$$最大半连通子图拥有的节点数$$K$$，以及不同的，最大半连通子图数目$$C$$

**算法分析**
怎么考虑？连通性问题的切入点，可以尝试考虑 DAG 的情形。
如果图是一个 DAG，那么所求的半连通子图$$G'$$就是$$G$$的**最长路**
`ans = 最长路长度`，同时`cnt = 最长路的条数`

如果是一般图呢？一般图就考虑**缩点**，缩点之后就是一个 DAG，怎么求拥有的节点数？
可以让**点带权**，每一个点权就是 SCC 的`size`，跑一遍`dp`求出最长路，并统计方案就可以

综上所述，需要先`SCC`缩点，然后让每一个点带权，权值为 SCC 的`size`，接着 dp 就可以

**算法实现**
在算法实现方面有一些细节要考虑

*  `DAG` 的 `dp` 需要考虑**拓扑序**，但是`Tarjan`算法的**出栈顺序**就是**反图的拓扑序**
    跑`Tarjan`得到的`SCC`编号实际上就是有向图反图的拓扑序
	
*   根据这一点，在 dp 的时候，只要按 SCC 编号顺序，可以保证当考虑$$dp(i)$$的时候，
    用那些已经被计算出来的$$dp(j)$$更新$$dp(i)$$，$$dp(i) \leftarrow dp(j)$$
	此时$$j$$这个连通分量，一定在`dfs`树中**更深**的位置
	
```bash
for i = every SCC:
    for SCC[i] 中的点 u，考虑边 (u, v)，如果 (u, v) 不属于同一个 SCC，j = (v 所在的 SCC)
	    dp(i) = max( dp(i), dp(j) )
		如果此时发现 dp(i) = dp(j)，说明两种方案都可以，way(i) += way(j)
	
	dp(i) += size(i)
```

* 其他编程注意事项，**缩点之后**，是会有**重边**的，需要用`vis`防止重边的情况，重边算方案时候只需要算一次
  `dfs`的时候如何考虑重边？可以用`vis`和**全局变量 T** 来标记
  
  ```bash
  int T = 0;
  for i in Vertex:
      vis[i] = ++T
	  这样当且仅当 vis[j] != T 的时候，表示 j 这个点未被访问过，否则就是访问过了
	  
	  if (vis[j] != T):		vis[j] = T,  访问 T
  ```
  
**综上所述**，`DAG`的`dp`过程大致如下
```bash
T 全局变量来判断重边
for i = every SCC
    dp[i] = 0, way[i] = 1, vis[i] = ++T
	
	for SCC[i] 中的所有点 u，检查边 (u, v)，考虑 v 所在的 SCC，j = bel[v]
		if vis[j] != T  and  j != i:
			dp(i) = max(dp(i), dp(j))
			if (dp(i) == dp(j)):		way(i) += way(j)
			
	
	dp(i) += size(i),
	
	ans 保存答案，wans 保存方案
	if ans < dp(i):		ans = dp(i), wans = 0
	if ans == dp(i):   wans += way(i)
```

## 抢劫计划 ATM
**[抢劫计划](https://ac.nowcoder.com/acm/problem/211213)**
$$(N, M)$$的有向图，有向图中的节点表示 ATM 取款机，有的节点还有酒吧
劫匪计划从市中心开始抢劫，市中心编号是$$s$$，他沿着单向路行驶，把路过的 ATM 都抢了
最后会停在某一个酒吧，但具体哪个不确定，一个点可以被经过任意多次，但抢劫一次 ATM 之后，这个点就没钱了
现在给定每个 ATM 的现金数，问最多能抢多少？

**算法分析**
切入点还是，对于有向图，考虑`SCC`缩点成`DAG`，点带权，权值为`SCC`中点的金额
然后考虑`dp`，只不过这里的`dp`是有限制的
如果某个`SCC`中没有酒吧，那么劫匪不能停下，要继续走，怎么处理这个限制？

不难发现，用缩点后的 DAG 跑 dp，`for i = 1 to cnt`，我们用**更深的点**来更新**较浅的点**
也就是说，如果从某个深度的点$$i$$往下，都没有酒吧，那么这些 SCC 的钱都不能抢，要舍弃
实际上，就是考虑如果`[1...i]`这些点都没有酒吧，就不计数
基于这种分析，可以在`for i = 1 to cnt 遍历 SCC`的时候，$$dp_i \leftarrow -\infty$$，初值都设为$$-\infty$$

```bash
for i = every SCC:
     for SCC[i] 中的点 u，若 (u, v) 并且 v 不在 SCC[i] 中，j = bel[v]
	 		dp(i) = max( dp(i), dp(j) )
			
	if SCC[i] 中有酒吧:		dp(i) = max( dp(i), 0 )
	dp(i) += （SCC 的权值和）
```

## 所驼门王的宝藏
**[SDOI 2010 所驼门王的宝藏](https://ac.nowcoder.com/acm/problem/20338)**
**问题描述**
给定一个$$R \times C$$的矩阵，有$$N$$个点有宝藏，宝藏房有传送门，只能通过传送门，从一间房走到另一间
传送门有`3`种，分别是，可以传到同一行任意房间，同一列任意房间，以及以该房间为中心的周围8个房间
自行确定起点和终点，问能够获得最多多少个不同的宝藏（最长路）

**算法分析**
这个问题的技巧在与建图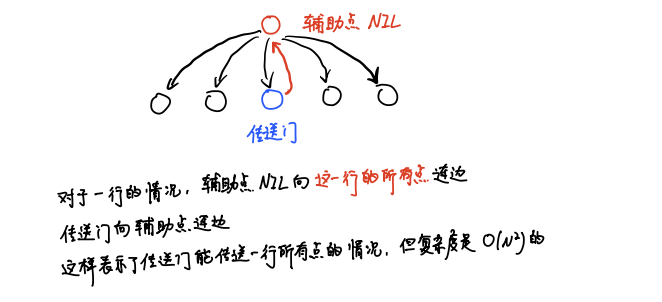
![](/media/content_img/SDOI2010.png)

行和列的情况，都可以用**辅助点**的方法，降低连边的数量，从而表示出，
传送门可以到达一行（列）所有点的情况
至于四周八个点，这种情况最多就`8`个点，暴力处理就可以

>  建图完成后，如何计算？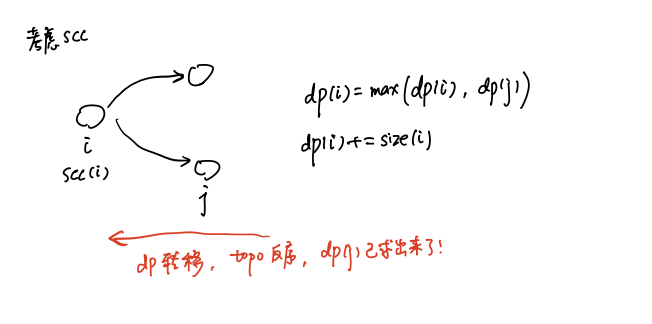

![](/media/content_img/DAGdp.png)

如上图所示，先进行缩点，缩点的同时计算出每一个 SCC 的`size`，之后考虑 DAG 的 dp
值得注意的是，统计`size`的时候，不需要考虑**辅助点**

看完文章有啥想法

算法小站

wiki 主题

图论

有向图强连通分量

目录