wiki - 算法小站

wiki 主题

主题名称

是否为父主题

是否为其添加wiki文章

选择主题

修改主题名称

修改父主题

修改wiki文章

算法基础搜索数据结构字符串数学图论动态规划计算几何杂项

杂项

启发式合并

高精度

[[ item.c ]]

高精度

```bash
class BigInt {
#define Value(x, nega) ((nega) ? -(x) : (x))
#define At(vec, index) ((index) < vec.size() ? vec[(index)] : 0)

public:
    mutable vector<long long> val;
    const static long long Mod = 1000000000;
    const static int exp = 9;
    mutable bool nega = false;

void trim() const {
        while (val.size() && val.back() == 0) val.pop_back();
        if (val.empty()) nega = false;
    }
    int size() const { return val.size(); }
    long long &operator[] (int idx) const { return val[idx]; }

BigInt(int size, bool nega) : val(size), nega(nega) {}
    BigInt(const vector<long long> &val, bool nega) : val(val), nega(nega) {}

BigInt(long long x = 0) {
        if (x < 0) {
            x = -x, nega = true;
        }
        while (x >= Mod) { val.push_back(x % Mod), x /= Mod; }
        if (x) val.push_back(x);
    }

BigInt(const string &str) {
        int bound = 0, pos;
        if (str[0] == '-') nega = true, bound = 1;

long long cur = 0, pow = 1;
        for (pos = str.size()-1; pos >= bound + exp - 1; pos -= exp, val.push_back(cur), cur = 0, pow = 1) {
            for (int i = pos; i > pos - exp; --i) {
                cur += (str[i] - '0') * pow, pow *= 10;
            }
        }

for (cur = 0, pow = 1; pos >= bound; pos--) {
            cur += (str[pos] - '0') * pow, pow *= 10;
        }
        if (cur) val.push_back(cur);
    }

// [0...cap], low -> high
    BigInt &operator += (const BigInt &rhs) {
        const int cap = max(size(), rhs.size()) + 1;
        val.resize(cap);

int carry = 0;
        for (int i = 0; i < cap-1; ++i) {
            val[i] = Value(val[i], nega) + Value(At(rhs, i), rhs.nega) + carry, carry = 0;

if (val[i] >= Mod) val[i] -= Mod, carry = 1;
            else if (val[i] < 0) val[i] += Mod, carry = -1;
        }

if ((val.back() = carry) == -1) {
            nega = true, val.pop_back();
            bool trailZero = true;
            for (int i = 0; i < cap-1; ++i) {
                if (trailZero && val[i]) {
                    val[i] = Mod - val[i], trailZero = false;
                }
                else if (val[i]) {
                    val[i] = Mod - 1 - val[i];
                }
            }
        }
        trim();
        return *this;
    }
    friend BigInt operator+ (const BigInt &lhs, const BigInt &rhs) {
        BigInt ret(lhs);
        return ret += rhs;
    }
    friend BigInt operator- (const BigInt &lhs, const BigInt &rhs) {
        BigInt ret(lhs);
        return ret -= rhs;
    }
    
    friend BigInt operator- (const BigInt &rhs) {
        BigInt ret(rhs);
        ret.nega ^= 1;
        return ret;
    }
    BigInt &operator -= (const BigInt &rhs) {
        rhs.nega ^= 1;
        *this += rhs;
        rhs.nega ^= 1;
        return *this;
    }

friend BigInt operator* (const BigInt &lhs, const BigInt &rhs) {
        const int cap = lhs.size() + rhs.size() + 1;
        BigInt ret(cap, lhs.nega ^ rhs.nega);

for (int i = 0; i < cap-1; ++i) {
            for (int j = max(i-rhs.size()+1, 0), up = min(i+1, lhs.size()); j < up; j++) {
                ret[i] += lhs[j] * rhs[i - j];
                ret[i + 1] += ret[i] / Mod, ret[i] %= Mod;
            }
        }
        ret.trim();
        return ret;
    }
    BigInt &operator *= (const BigInt &rhs) { return *this = *this * rhs; }

friend BigInt operator/ (const BigInt &lhs, const BigInt &rhs) {
        // 用倍增加法来实现
        // estimate(i)，位权值，对应 2^i * estimate(i)
        
        vector<BigInt> powTwo {BigInt(1)};
        vector<BigInt> estimate;
        estimate.clear();

if (abscmp(lhs, rhs) < 0) return BigInt();

BigInt cur = rhs;
        int cmp;
        
        while (( cmp = abscmp(cur, lhs) ) <= 0) {
            estimate.push_back(cur), cur += cur;
            if (estimate.size() >= powTwo.size()) powTwo.push_back( powTwo.back()+powTwo.back() );
        }
        if (cmp == 0) return BigInt(powTwo.back().val, lhs.nega ^ rhs.nega);

BigInt ret = powTwo[ estimate.size()-1 ];
        cur = estimate[ estimate.size()-1 ];

for (int i = estimate.size()-1; i >= 0 && cmp != 0; --i) {
            if ( (cmp = abscmp(cur + estimate[i], lhs)) <= 0 ) {
                cur += estimate[i], ret += powTwo[i];
            }
        }
        ret.nega = lhs.nega ^ rhs.nega;
        return ret;
    }

static int abscmp(const BigInt &lhs, const BigInt &rhs) {
        if (lhs.size() != rhs.size()) {
            return lhs.size() < rhs.size() ? -1 : 1;
        }
        for (int i = lhs.size()-1; i >= 0; --i) {
            if (lhs[i] != rhs[i]) return lhs[i] < rhs[i] ? -1 : 1;
        }
        return 0;
    }

bool operator== (const BigInt &rhs) const {
        return nega == rhs.nega && val == rhs.val;
    }
    bool operator!= (const BigInt &rhs) const { return nega != rhs.nega || val != rhs.val;  }
    bool operator>= (const BigInt &rhs) const { return !(*this < rhs); }
    bool operator> (const BigInt &rhs) const { return !(*this <= rhs); }

bool operator<= (const BigInt &rhs) const {
        if (nega && !rhs.nega) return true;
        if (!nega && rhs.nega) return false;
        int cmp = abscmp(*this, rhs);
        return nega ? cmp >= 0 : cmp <= 0;
    }

bool operator< (const BigInt &rhs) const {
        if (nega && !rhs.nega) return true;
        if (!nega && rhs.nega) return false;
        return (abscmp(*this, rhs) < 0) ^ nega;
    }

void swap(const BigInt &rhs) const {
        std::swap(val, rhs.val);
        std::swap(nega, rhs.nega);
    }

friend std::ostream &operator<< (std::ostream &os, const BigInt &x) {
        if (x.size()) {
            if (x.nega) cout << "-";
            for (int i = x.size()-1; i >= 0; --i) {
                if (i == x.size() - 1) cout << x[i];
                else cout << std::setw(exp) << std::setfill('0') << x[i];
            }
        }
        else {
            cout << "0";
        }
        return os;
    }
};
```

## 高精度加减
从**低位往高位做**，压位之后，还需要一个`carry`来维护进位或者是借位
如果`carry > 0`，表示**进位**，否则表示**借位**

> 回顾一下普通的借位
```bash
if (c[i] < 0) {
	c[i + 1] -= 1;
	c[i] += Mod;
}
```

这里我们把加法和减法运算统一起来，如果做完了最高位，发现`carry = -1`，即`(val.back() = carry) = -1`
那么说明我们做的是$$a - b$$，并且$$a - b < 0$$
但高精度我们每一位存的是$$(M + a - b) \bmod M$$，这不是我们想要的结果
我们实际上想要得到的是$$-|b - a|$$，符号位我们单独维护，我们需要的是$$b - a$$

只需要令$$M - (M + a - b)$$即可，而$$M+a-b$$是我们已经求出来的结果
所以$$M - val[\cdots]$$即可，那么我们一位一位来看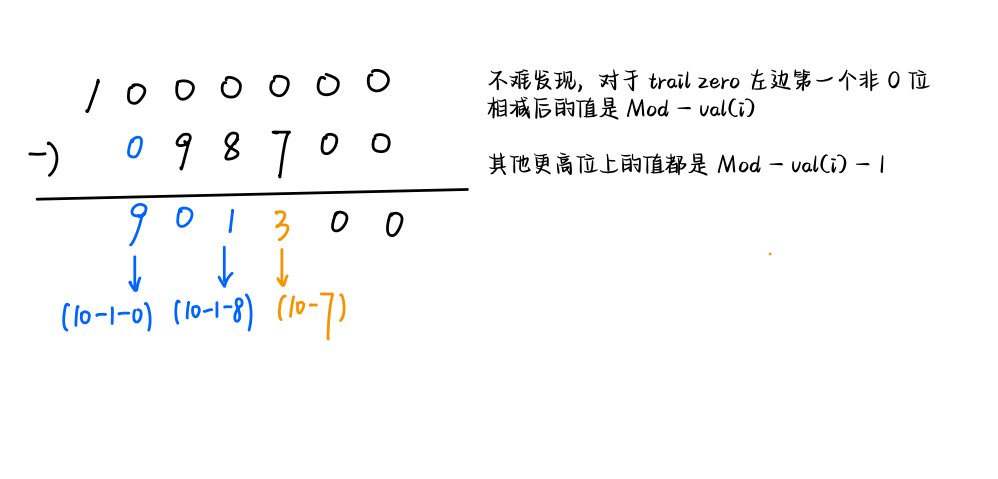
![](/media/content_img/BigInt01.png)

## 高精度乘除
**用倍增维护高精度除法**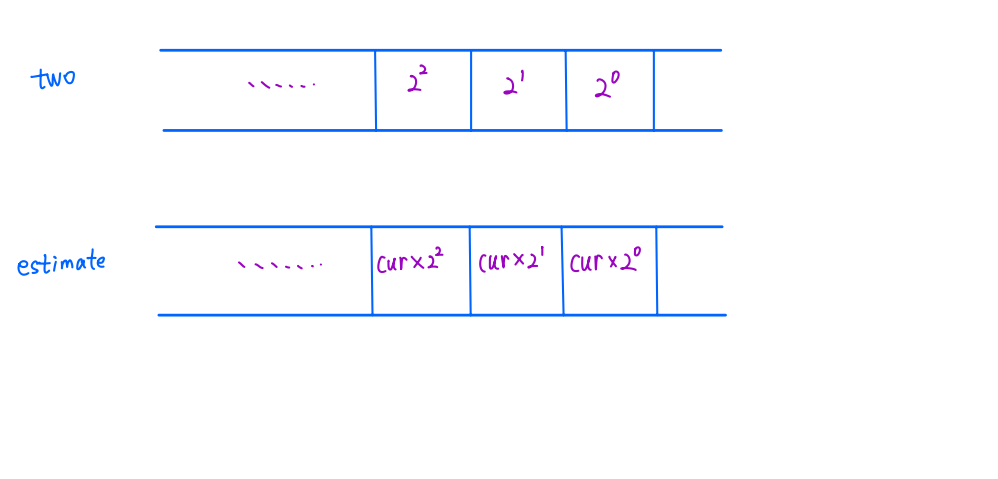
![](/media/content_img/BigInt02.png)

> 对于$$\text{lhs} / \text{rhs}$$，令$$\text{cur} = \text{rhs}$$，不断倍增$$\text{cur}$$，使其接近$$\text{lhs}$$

维护倍增数组（关于$$2^?$$），和估计值数组`estimate`，我们用`estimate`的值，倍增去逼近`lhs`

令`cur = rhs`，只要`while cur <= lhs`，就应该`estimate.push_back(cur), cur += cur`，同时维护`two`数组
如果`estimate.size() >= two.size(), two.push_back( two.back() + two.back() )`
这样就维护好了倍增数组，以及对应的值数组
同时我们可以知道，**最大的不超过`lhs`的数**，就是`estimate[ size()-1 ]`

如果此时已经有`estimate.back() == lhs`，那么说明已经做完了，`two.back()`就是答案

否则，除法的结果（商）是若干个二进制的组合，比如$$2^? + 2^? + \cdots + 2^?$$
我们从**较大的二进制幂指，往较小的去找**，和倍增逻辑一样
令`cur = estimate.back()`，`cur`还要加上一些数才能和`lhs`相等
同时维护`two`，一开始`ret = two.back()`，`ret`也要同步加上$$2^?$$才能和商（答案）相等

`for i = size()-1 downto 0`，如果发现`cmp == 0 (即 cur == lhs)`，那么就可以退出循环了
否则，只要`( cmp = abscmp( cur + estimate[i] ) ) <= 0`，那么我们就应该把第$$i$$位的值加上
`cur += estimate[i], ret += two[i]`

> 特别说明，最后可能除不尽，到`i = 0`也不会有`cmp == 0`成立，但倍增的时候
我们已经把**能加的都加上去**了，最后`ret`一定是$$\lfloor \dfrac{lhs}{rhs} \rfloor$$

看完文章有啥想法

算法小站

wiki 主题

杂项

高精度

目录