算法小站
首页
wiki
新鲜事
文章搜索
网站导航
回忆录
首页
wiki
新鲜事
文章搜索
网站导航
回忆录
登录
注册
算法基础
搜索
数据结构
字符串
数学
图论
动态规划
计算几何
杂项
codeforces上的dp题(四)
有一个dp技巧比较重要,当存在一个dp值能够转移连续一段的时 .....
[[ slider_text ]]
[[ item.c ]]
0
0
codeforces上的dp题(四)
发布时间
2024-10-30
作者:
秋千月
来源:
算法小站
扫描线
dp
## Codeforces Round 959 **[Codeforces Round 959 C. Hungry Games](https://codeforces.com/contest/1994/problem/C)** **问题描述** 给你$$n$$个蘑菇,每个蘑菇的毒性是$$a_i$$,然后你可以选一段区间$$[l, r]$$ 从左到右吃蘑菇,你有一个初始耐毒值$$g = 0$$,并且还有一个$$x$$,是最大耐毒值 如果你遇到毒性为$$k$$的蘑菇并且吃掉,那么会发生一些事情 首先,$$g$$的值会增加$$k$$ 如果$$g > x$$,那么$$g$$会清$$0$$ 现在问你有多少种选择方式,选择$$[l, r], 1 \leqslant l \leqslant r \leqslant n$$ 使得最后$$g$$不是$$0$$ ### 算法分析 枚举左端点$$i$$,看它最远能扩展到哪个位置?如果发现$$sum[i, j] > x$$ 说明在$$j$$这个位置,$$g$$值清$$0$$,另外$$[i, j-1]$$就是合法的区间,右端点有$$(j - i)$$种选择 另外,还能不能继续选?因为$$a_i \geqslant 1$$,实际上$$[j+1, j+2, \cdots]$$都是可以被选作右端点的 注意到这里$$j+1$$右作为新的左断点,**重新开始计算了** 问题又转化为,从$$j+1$$能继续往后选几个位置? 这就是很**明显的 dp 了** 二分$$j \in [i, n+1]$$,如果$$j = n+1$$,那么$$dp(i) = n-i+1$$ 否则,$$dp(i) = dp(j+1) + (j-i)$$ ## Educational Codeforces Round 166 **[Educational Codeforces Round 166 C. Job Interview](https://codeforces.com/contest/1976/problem/C)** **问题描述** 有$$n+m+1$$个候选人,要选$$n$$个程序员和$$m$$个测试员 每个人有编程技能$$a_i$$和测试技能$$b_i$$,现在要你尽可能让团队的能力最大化 即$$n$$个程序员编程能力的和,加上$$m$$个测试员编程能力的和 输出$$i$$个值,表示万一$$i$$号员工没来面试,团队能够获取的最大编程能力的和 注意,**职位的分配符合先来先选**,也就是说,越靠前的人,如果$$a_i > b_i$$,那么会让他做程序员 如果程序员已满,或者他更擅长测试,那么他会被分去做测试员,**一个萝卜一个坑** ### 算法分析 由于选人遵循**先来先选**的原则,假设**不删人**,那么模拟一遍,得到$$res$$ 一个萝卜一个坑,这个值就是$$n+m+1$$位置的答案 > 接下来考虑删人 不难发现,删去某个位置$$i$$,我们要关注的是$$[i+1\cdots n]$$**右边第一个未能得偿所愿的人的位置** 那么可以讨论一下 1)假设所有人都得偿所愿,那么删去的$$i$$,原来从事的工作就由$$n+m+1$$位置的人代替 2)否则的话,假设$$i$$原来是从事工作$$1$$的,那么就要找到第一个**本来想从事工作1,却被迫从事工作2的人** 让这个人来接替工作 3)但问题是,一个萝卜一个坑,如果找到这样的人$$p$$来接替工作,很可能$$p$$后面的人的工作都要更换 这个问题也比较好解决,记一下每个位置$$i$$,$$dp(i)$$表示后缀$$[i+1\cdots n]$$**换工作的代价和** 假设需要换工作的人是$$p_1, p_2\cdots$$,那么$$dp(p_1) = dp(p_2) + a(p_1) - b(p_2)$$ 这里假定删掉的人原先从事工作$$a$$,$$p_1$$原先**不情愿地选择工作$$b$$,现在接替$$i$$从事工作$$a$$** 这里$$p_1, p_2$$都是记录**未能得偿所愿的人** > 具体到算法实现上 令$$pa$$维护右边第一个想从事$$a$$工作,现实却从事其他工作的人 令$$pb$$维护右边第一个想从事$$b$$工作,现实却从事其他工作的人 一开始另$$pa = n+m+1, pb = n+m+1$$,此时除了最后一个人没肉吃,其他所有人都能得偿所愿 对后缀从后往前扫描,对于某个$$i$$ 1)如果$$i$$从事的是$$a$$,并且$$pa = n+m+1$$,说明后面所有人都没有特别想从事$$a$$工作 这个工作就只能交给最后来的人,有转移$$dp(i) = dp(pa) + a(pa)$$ 如果$$i$$从事的是$$b$$工作,并且$$pb = n+m+1$$,也是同样$$dp(i) = dp(pb) + b(pb)$$ 2)否则,其他情况都是有未能得偿所愿的人 如果$$i$$从事的是$$a$$工作,那么就要找到那个**本来特别想从事$$a$$工作的那个人**$$pa$$ 令$$dp(i) = dp(pa) + a(pa) - b(pa)$$(因为这个人本来想从事$$a$$,却不得已从事$$b$$) 另一种情况也是类似,$$dp(i) = dp(pb) + b(pb) - a(pa)$$ 3)然后尝试更新$$pa, pb$$,如果$$a_i > b_i$$但是`chose(i) = 1`,说明$$i$$本来想干$$a$$,却做了$$b$$ 更新$$pa = i$$,另一种情况也是类似的 4)最后的答案,对于$$i$$,结果就是`res - (i 的职业代价) + dp(i)`,$$dp(i)$$表示调整后缀需要**改变的总代价** ## Codeforces Round 809 (Div. 2) **[Codeforces Round 809 (Div. 2) C. Qpwoeirut And The City](https://codeforces.com/problemset/problem/1706/C)** **问题描述** 给你一个长度为$$n$$的序列,第$$i$$个比第$$j$$个高,当且仅当$$h_i > h_j$$ 一个建筑是漂亮的,当且仅当它的高度高于$$i-1$$和$$i+1$$,另外,两端的建筑不可能是漂亮的 现在可以在建筑上方增加楼层数,使得漂亮的建筑数量最多,现在要你最小化添加楼层的数量 ### 算法分析 非常典型的$$dp$$,方程也很好写,$$0/1$$表示是否是漂亮建筑 $$dp(i-1, 1) \to dp(i, 0)$$ $$dp(i-1, 0) + \Delta \to dp(i, 1)$$,如果$$a\_i > \max(a\_{i-1}, a\_{i+1})$$,那么$$\Delta = 0$$ 否则$$\Delta = |a\_i - \max(a\_{i-1}, a\_{i+1})| + 1$$ > 这样咋一看是对的,但是第四个样例给出了特殊情况 注意到$$n$$为偶数的时候,存在着两个$$0$$紧挨着的情况,但注意到,这样紧挨的位置有且仅有一个 所以我们再引入一个状态$$k = 0/1$$,记录是否发生过**紧挨行为** 当且仅当$$n$$偶数的时候,我们有$$dp(i-1, 0, 0) \to dp(i, 0, 1)$$ 剩下的转移都不变 ## Codeforces Round 940 (Div. 2) **[Codeforces Round 940 C. How Does the Rook Move?](https://codeforces.com/contest/1957/problem/C)** **问题描述** 你和电脑轮流放置黑白棋,要确保没有两个棋子会互相攻击 互相攻击的条件是,两个棋子位于同一行或者同一列(不管颜色) 你能在$$(r, c)$$放一个白棋的充要条件,是它不会攻击其他棋子 然后电脑镜像在$$(c, r)$$放一个黑棋,如果$$r = c$$,那么电脑跳过这一步 那么现在假设你已经走了$$k$$步,并且电脑复制了$$k$$个镜像 你要继续走,直到没有办法走为止,现在问最终状态有多少种不同的棋局? 两个棋局是不同的,当且仅当存在一个$$(r, c)$$,使得它在一个棋局中有棋子,另一个棋局中没有棋子 或者是两个棋局中,这个位置的棋子颜色不同 输入给出$$k$$,并且给出$$(r_i, c_i)$$表示第$$i$$步在哪里放棋子 ### 算法分析 注意到我们只关心方案数,并不关心棋子的具体位置 假设说我们不在$$r = c$$的位置放棋子,那么原来是$$x \times x$$的问题,转化成$$(x-2) \times (x-2)$$的子问题 如果在$$r = c$$位置放棋子,那么问题转化成$$(x-1)\times (x-1)$$的子问题 不妨考虑$$dp$$,用$$eq$$记录一下有几个形如$$(r = c)$$的位置可以放置 那么有如下转移 ```math \displaystyle dp(x, eq) \leftarrow dp(x-1, eq-1) \cdot \binom{eq}{1} \\ dp(x, eq) \leftarrow dp(x-2, eq) \cdot \binom{x^2 - eq}{1} ``` 但是这样做是会**重复**的,对于一个位置$$p$$,在 dp 的第$$k$$阶段放棋子, 和在第$$k+1\cdots$$阶段放棋子,最后会造成一样的局面,这个问题怎么解决呢? 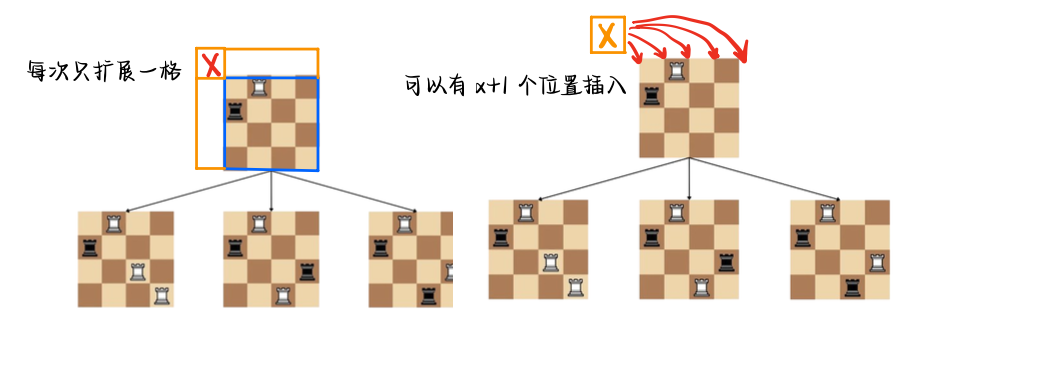 实际上,原问题相当于,我们已经解决完$$(x-2)$$或者$$(x-1)$$规模的问题 然后在棋盘上插入一个白棋(实际上是相当于插入一列),并且只在最上方(或者最左端)插入 1)对于$$x-1$$规模的问题,我们只能放置在$$r = c$$位置,也就是说新插入的棋子只能在$$(1, 1)$$,方案数唯一 这种情况有转移$$dp(x) \leftarrow dp(x-1)$$ 2)对于$$x-2$$规模的问题,我们可以把白棋放在最上方,也就是第$$1$$行 第$$1$$行可以放$$x-1$$个位置(相当于插入 1 列,有$$x-1$$个位置可以插入) 当白棋放置完毕之后,黑棋的位置也随之确定,黑棋就位于最左边的一列,也就是第$$1$$列 当然对应的位置仍然可以取$$1 \sim x-1$$所有的位置 白棋和黑棋的位置可以对调,有转移$$dp(x) \leftarrow 2 \cdot (x-1) \cdot dp(x-2)$$ 状态转移方程,可以用记忆化求解 ## Codeforces Round 951 (Div. 2) **[Codeforces Round 951 (Div. 2) D. Fixing a Binary String](https://codeforces.com/contest/1979/problem/D)** **问题描述** 给定一个01字符串,你能执行一下操作,恰好一次 选择一个下标$$1 \leqslant p \leqslant n$$,翻转$$s[1\cdots p]$$,$$s[p+1\cdots n]$$保持不变 然后看成一个循环串,左移$$p$$次,构成$$s[p+1\cdots n] + s[p\cdots 1]$$ 定义一个串是 k-proper,当且仅当 首先,$$s_1 = s_2 = \cdots = s_k$$ 其次,对于$$1 \leqslant i \leqslant n-k$$,有$$s(i+k) \neq s(i)$$ 比如,如果$$k = 3$$,那么 k - proper 串一定是形如`[111][000][111]...`这样一段一段的 现在给你一个数$$k$$,保证$$k$$是$$n$$的因子,需要找到这个数$$p$$ 使得执行操作之后,字符串变成 k-proper,注意到如果一开始串就是 k-proper ,你也需要执行一次这样的操作 ### 算法分析 > 先考虑什么情况下一定不行? 观察后发现,我们记录字符串**最后的,相同字符的个数**$$tail$$,如果$$tail > k$$,那么一定不行 否则的话,我们要去前面找,**最后相同字符个数等于**$$\Delta = k - tail$$的前缀 假设找到这个位置为$$p$$,我们要看一下$$[1\cdots p-\Delta]$$和$$[p+1\cdots n-tail]$$是否合法 这可以正着扫描一遍,倒着扫描一遍,记录每个位置是否合法来实现 > 算法实现上 用$$bad1(i), bad2(i)$$分别表示前缀$$[1\cdots i]$$,后缀$$[i\cdots n]$$是否合法 做的时候,用两个哈希表`mp0[ tail ] = {j1, j2, ...., jk}, mp1[ tail ] = {j1, j2, ...., jm}` 分别表示结尾有`tail`个`0/1`的**前缀**的位置 这个很好实现,用`num[0/1]`记录一共有几个连续的`0/1`即可 如果发现`str[i] != str[i+1]`,看一下连续的`num[ 0/1 ]`的个数,如果$$\neq k$$,那么说明这个前缀不合法 同时不论如何,这会开启一个新的段,记得对`num[ 0/1 ]`清空 否则的话,如果发现`num[0/1] > k`,那么这一段前缀也不合法 这样就可以计算出`bad1[ 1....n ], bad2[ 1....n ]`每个位置是否合法 ## Codeforces Round 982 (Div. 2) **[D2. The Endspeaker (Hard Version)](https://codeforces.com/contest/2027/problem/D2)** **问题描述** 给定两个序列`a[1...n], b[1...m]`,一开始$$k$$的值是$$1$$,你的目标是清空$$a$$数组,可以用以下操作 第一,增加$$k$$的值,这不需要额外代价 第二,删掉$$a$$的一个**非空前缀**,必须满足**非空前缀的和**$$\leqslant b_k$$,代价$$m-k$$ 现在问清空$$a$$数组的最小代价 ### 算法分析 不难想到用动态规划,因为$$k$$是从$$1$$开始增加的,需要从$$k\in [1\to m]$$开始做 令$$k \in [1\to m], i \in [1 \to n]$$,$$dp(k, i)$$表示$$[1\cdots i]$$的前缀已经全部删去的最小代价 假设当前正在考虑删$$[i\cdots j]$$,**贪心地**,反正都是用$$b_k$$来删 那我们就看最多能从$$i$$开始删到哪里?$$j$$是$$[i\cdots n]$$中**最后一个满足**$$s(j) - s(i-1) \leqslant b_k$$的位置(二分可解决) ```math dp(k, i-1) \to dp(k+1, i-1) \\ dp(k, i-1) + (m - k) \to dp(k, j) ``` > 难的是统计方案 注意到,统计方案的时候,对于$$dp(k, i-1)$$,均可以转移到$$j1\in [i,i+1,\cdots, j]$$ 均有合法转移$$dp(k, i-1) + (m - k) \to dp(k, j1)$$ 一种暴力的方法是`for j1 = [i...j]`,把这些转移都统计一遍,怎么优化呢? **当存在一个dp值,能够转移到连续一段的时候**,考虑使用**扫描线** > 扫描线怎么做? 用$$evt(k, i)$$记录这个状态能够出现的,所有可能的 dp 值,记`type`为事件的类型 那么`evt(k, i) = { (type1, dp1, way1), (type2, dp2, way2), ..... }` 大致思路是,检查`evt(k, i)`中所有的事件,加的加,减的减,然后找到`dp`值最小的那个事件`(dpv, way)` 计算转移后的新的`dp`值,新的方案`(ndpv, nway)`,然后更新区间`[i+1...j]` 令`evt(k, i+1).push_back( {0, ndpv, nway} ), evt(k, j+1).push_back( {1, ndpv, nway} )` 在$$i$$位置加,在$$j+1$$位置减,这是**扫描线思路** > 怎么统计方案 转移的时候,我们需要记录当前可能的所有$$dp$$值,它们对应的**方案数** 假设有转移$$dpv1 \to dpv2$$,更新方案数`f( dpv2 ) += f( dpv1 )`,可以用一个`map`记录 但注意到,因为我们用扫描线,还需要统计一下当前这个**dp值出现的次数** 如果出现的次数为$$0$$,在`map`中及时把它删掉 用`map<ll, mint> f`记录方案,`f( dpv ) = { num, dpway }`,当`num = 0`的时候,`f.erase(dpv)` 在遍历到$$evt(k, i)$$的时候,首先检查一下**这个位置挂载了哪些 dp 值**?不妨设`(type, dpv, way)` 接下来该加加,该减减 如果`type = 1`,那么更新`f(dpv).num += 1, f(dpv).dpway += way` 否则更新`f(dpv).num -= 1, f(dpv).dpway -= way`,如果`num = 0`,删去`dpv` 更新完成之后,取出`*f.begin()`,`dp(i, k) = ( dpv, f(dpv) )` 接着考虑两种转移 第一种是`(dpv, f(dpv))`,转移到$$(k+1, i)$$这个位置,扫描线执行 `evt(k+1, i).push_back( {0, dpv, f(dpv)} ), evt(k+1, i+1).push_back( {1, dpv, f(dpv)} )` > 说明,扫描线的话,不必考虑重复计算的问题,因为$$i \to i+1$$的时候,在`i`处对应的`(dpv, way)` 在$$i+1$$处一定有**事件**`{1, dpv, way}`,相应的`f(dpv).dpway -= way`,方案数会被扣除 只要考虑`f(dpv) = { num, dpway }`,`num`作为计数器,当`num = 0`的时候,把对应的`dpv`及时从 map `f`中**删掉**,即可保证算法的正确 第二种是`(dpv + m - k, f(dpv))`,这时候是**区间转移**,转移到$$[i+1, j]$$中 执行`evt(k, i+1).push_back( {0, dpv+m-k, f(dpv)} )` 另外`evt(k, j+1).push_back( {1, dpv+m-k, f(dpv)} )` 最后统计答案 答案我们新开一个`map<ll, mint> res`,然后把`for k = [1...m]`所有的`dp(k, n) = {dpv, dpway}` 它们出现的`dp`值全部统计起来,`res[dpv] += dpway` 最后取`res.begin()`就是答案 **特别注意** 第一,就是`evt`事件是全局有效的,但是对于$$k$$的统计,是独立的 也就是我们每遍历到一个新的$$k$$,都要清空(或者重新开一个`map`),单独记录 并统计,这个阶段,$$(k, i)$$下面**挂载**的所有事件,所有可能的**dp值** 第二,因为存在扫描线`evt(k+1, i).push_back()`的操作 而当$$i = n$$的时候,不会有新的转移了,也就是不会有**新事件产生**了,所以`i = n`的时候就可以`continue`了 ## EPIC Institute of Technology Round Summer 2024 **[D. World is Mine](https://codeforces.com/contest/1987/problem/D)** **问题描述** 给你$$n$$个面包,每一个面包有一个美味程度$$a_i$$,`Alice`和`Bob`轮流吃,`Alice`最先开吃 `Alice`会选择任意一个**美味程度严格大于**`max( Alice 已经吃过的面包的美味程度 )`的面包 而`Bob`会选择剩下的,任意的面包 两个人都足够聪明,`Alice`想让自己吃的面包数$$x$$进可能大,而`Bob`想让$$x$$尽可能小 问$$x$$最后是多少(即`Alice`吃的面包最多有多少个) ### 算法分析 一个很明显的观察就是,**假设所有面包的种类都不同**,那么就不存在博弈,最后$$x = \lfloor \dfrac{n}{2} \rfloor$$ > 现在假设有相同的面包,排序后,不妨设编号为$$i$$的面包有$$c_i$$个,考虑最优策略 假设当前考虑到$$i$$了,那么假设 Bob 不做干扰,那么 Alice 能够吃到`[1...i]`所有的面包 现在有了`Bob`的干扰,导致`[1...i]`中有些面包`Alice`吃不到,想两个问题 > Alice 吃不到面包的充要条件是什么?怎么样最大化**吃不到**? 实际上,我们只需要最大化**吃不到**,因为考虑到$$i$$的时候,没有`Bob`的干扰 Alice 是一定可以吃到`[1...i]`所有的面包的 那么 Bob 吃的面包数量$$j \leqslant i$$ 定义$$dp(i, j)$$表示当前$$i$$阶段,Bob 吃掉了$$j$$个面包,但是这个操作使得`[1...i]`中有些面包吃不到 此时最大的**吃不到数量**就是 dp 值 存在状态转移 如果 Bob 不拿面包$$i$$,那么$$dp(i, j) \leftarrow dp(i-1, j)$$ 如果 Bob 拿了面包$$i$$,那么$$dp(i, j) \leftarrow dp(i-1, j-C_i) + 1$$ 这就是一个背包问题,很容易求解 注意的是,状态转移要满足一些限制,因为 Alice 先手,`Alice 能拿的面包数量 >= Bob 面包数量` 对于第二种转移而言,注意到此时的决策,是 Bob 在第$$i$$阶段拿走了$$i$$这种面包 那么实际上,到$$i$$为止,Alice 能拿的只有$$i-1-dp(i-1, j-C_i)$$这么多 那么对于到状态$$(i, j)$$的转移,应该有$$j \leqslant i-1-dp(i-1, j-C_i)$$ 答案就是$$|n| - \max_j(dp(n, j))$$ ## Educational Codeforces Round 171 **[D. Sums of Segments](https://codeforces.com/contest/2026/problem/D)** **问题描述** 令序列$$b = [S(1, 1), S(1, 2)\cdots, S(1, n), S(2, 2), \cdots, S(2,n), \cdots S(n, n)]$$ 给你$$n$$个询问,求区间和 ### 算法分析 就是前缀和,编程难度有点大  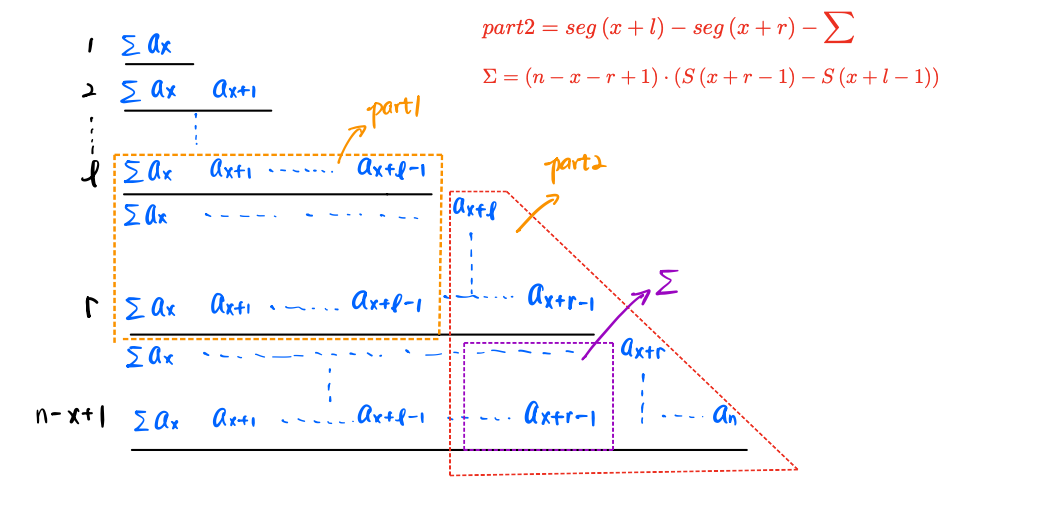
0
0
上一篇:codeforces上的dp题(三)
下一篇:杨氏矩阵(杨表)
看完文章有啥想法
发布评论
360 人参与,0 条评论