最大流和匹配

[[ slider_text ]]

[[ item.c ]]

发布时间 2024-12-13 作者：秋千月 来源：算法小站

流和匹配

## 最大流问题
### 流网络
一个源点和一个汇点，满足以下条件，边的容量为$$c(u, v)$$，流量为$$f(u, v)$$
1）容量限制，$$0 \leqslant f(u, v) \leqslant c(u, v)$$

2）流量守恒，除去源点和汇点，有$$\displaystyle \sum\_{v\in V} f(v, u) = \sum\_{u \in V} f(u, v)$$

3）流定义为$$|f| = \sum\_{v \in V} f(s, v) - \sum\_{v \in V}f(v, s)$$

### Ford-Fulkerson 方法
1）初始化流为$$f = 0$$
2）**while** 如果在残量网络中存在一条增广路径$$p$$，沿着$$p$$来增加流$$f$$
最后返回$$f$$

残量网络形式化定义如下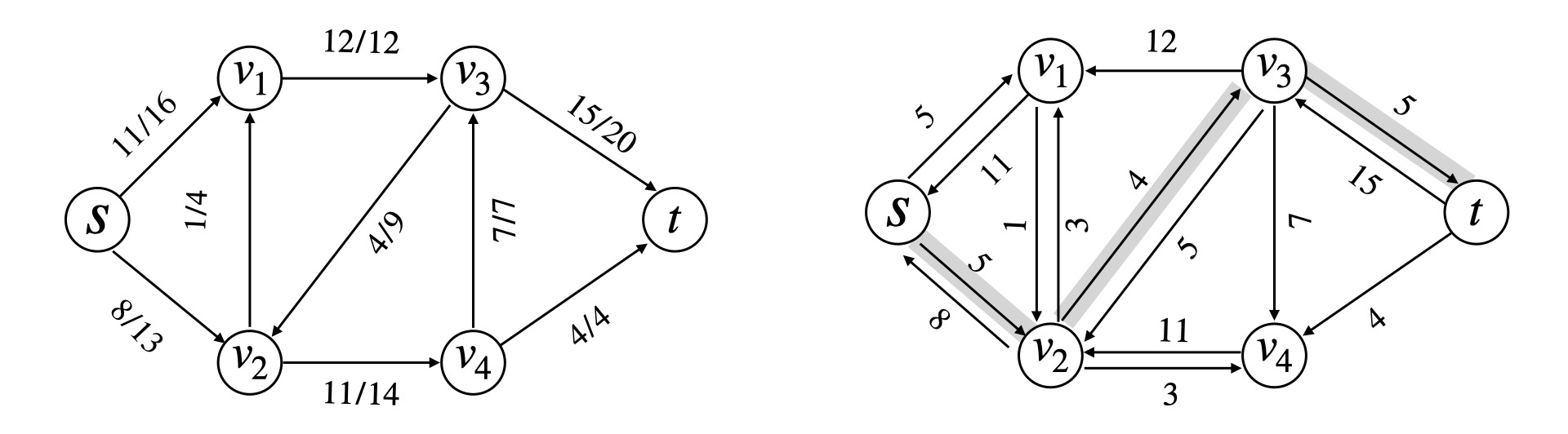
![](/media/content_img/flow01.jpg)
```math
c_f(u, v) = \begin{cases} c(u, v) - f(u, v)  & (u, v) \in E \\
f(v, u) & (v, u) \in E \\
0 & \text{other}
\end{cases}
```
定义$$f \uparrow f'$$为流$$f'$$对$$f$$的递增，那么
```math
(f \uparrow f')(u, v) = \begin{cases}
f(u, v) + f'(u, v) - f'(v, u) & (u, v) \in E \\
0 & \text{other}
\end{cases}
```

#### 引理 1
设$$G(V, E)$$是一个流网络，并且$$f$$是$$G$$的一个流，$$G_f$$是对应的残量网络，$$f'$$是$$G_f$$中的一个流
那么$$f \uparrow f'$$也是$$G$$中的一个流，并且$$|f \uparrow f'| = |f| + |f'|$$

> 证明如下

容量限制，$$f'(v, u) \leqslant c_f(v, u) = f(u, v)$$，从而
```math
(f \uparrow f')(u, v) = f(u, v) + f'(u, v) - f'(v, u) \geqslant f(u, v) + f'(u, v) - f(u, v) \\
= f'(u, v) \geqslant 0
```
同时还有
```math
(f \uparrow f')(u, v) = f(u, v) + f'(u, v) - f'(v, u) \leqslant f(u, v) + f'(u, v) \leqslant f(u, v) + c_f(u, v) \\
= f(u, v) + c(u, v) - f(u, v) = c(u, v)
```

流量守恒，对于所有非源汇节点
```math
\displaystyle
\sum_{v \in V} (f \uparrow f')(u, v) = \sum_{v \in V} ( f(u, v) + f'(u, v) - f'(v, u) ) \\
= \sum_{v \in V} f(u, v) + \sum_{v \in V} f'(v, u) - \sum_{v \in V} f'(u, v) \\
= \sum (f(v, u) + f'(v, u) - f'(u, v)) = \sum_{v \in V}(f \uparrow f')(v, u)
```

#### 引理 2
流量计算
不妨设$$V_1 = \\{v: (s, v) \in E\\}$$表示从源点$$s$$流出的流量，流量能到达的点的集合
令$$V_2 = \\{v: (v, s) \in E\\}$$表示流回源点$$s$$的流量，这些流量经过的点集

```math
\displaystyle
|f \uparrow f'| = \sum_{v \in V_1}(f \uparrow f')(s, v) - \sum_{v \in V_2}(f \uparrow f')(v, s) \\

= \sum_{v \in V_1}(f(s, v) + f'(s, v) - f'(v, s)) - \sum_{v \in V_2} (f(v, s) + f'(v, s) - f'(s, v)) \\

= \sum_{v\in V_1} f(s, v) - \sum_{v \in V_2} f(v, s) + \left( \sum_{v \in V_1} f'(s, v) + \sum_{v \in V_2}f'(s, v) \right) - \left( \sum_{v \in V_1}f'(v, s) + \sum_{v \in V_2} f'(v, s) \right) \\

= \left( \sum_{v \in V_1}f(s, v) - \sum_{v \in V_2} f(v, s) \right) + \left( \sum_{v \in V_1 \cup V_2}f'(s, v) - \sum_{v \in V_1 \cup V_2} f'(v, s) \right)
```
从而有$$|f \uparrow f'| = |f| + |f'|$$

### 增广路径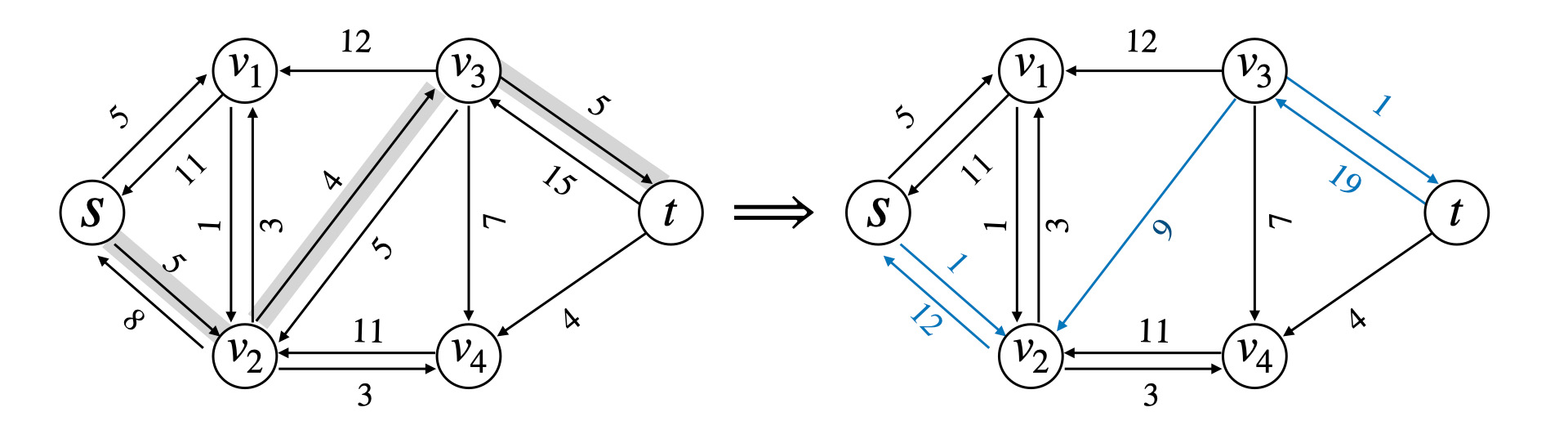
![](/media/content_img/flow02.jpg)
沿着增广路径走，注意$$G_f$$**反向边流量增加**
一条增广路径$$p$$能够给$$G$$每条边增加的流量最大值，是路径$$p$$的**残存容量**
```math
c_f(P) = \min c_f(u,v) \quad (u, v) \in P
```

设$$G = (V, E)$$为一个流网络，$$f$$为$$G$$中的一个流，设$$p$$是残量网络$$G_f$$的一条增广路径
```math
f_p(u, v) = \begin{cases} c_f(p)  & (u, v) \in p \\ 0 & \text{other}\end{cases}
```

## 流网络的切割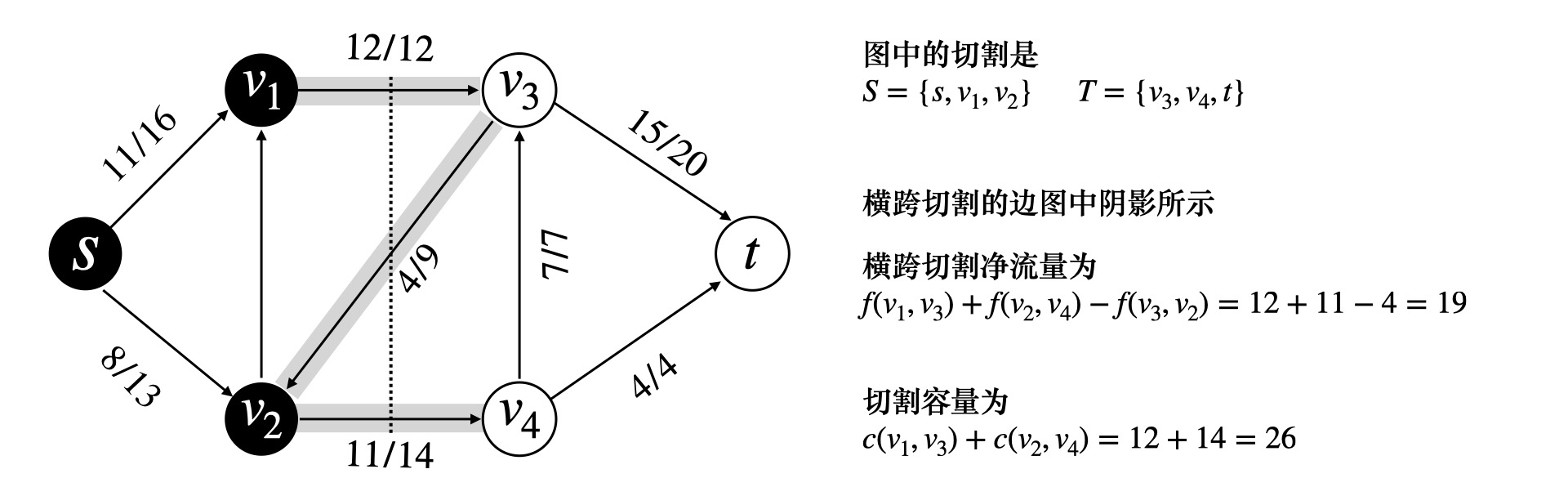
![](/media/content_img/flow03.jpg)

切割$$(S, T)$$将流网络划分成$$S,T$$两个集合，$$T = V - S$$，其中满足$$s \in S, t \in T$$
**净流量**
```math
\displaystyle
f(S, T) = \sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{u \in S}\sum_{v \in T} f(v, u)
```
**割的容量**
```math
\displaystyle
c(S, T) = \sum_{u \in S} \sum_{v \in T} c(u, v)
```
**引理**
设$$f$$为流网络$$G$$中的一个流，$$(S, T)$$是流网络的任意切割，那么横跨切割$$(S, T)$$的**净流量**总相同，$$f(S, T) = |f|$$

> 证明如下

首先，根据**流量守恒**
```math
\displaystyle
u \in V - \{s,  t\}: \quad \sum_{v \in V}f(u, v) - \sum_{v \in V}f(v, u) = 0
```
再对$$u \in S - \\{s\\}$$求和
```math
\displaystyle
\sum_{u \in S - \{s\}} \left( \sum_{v \in V}f(u, v) - \sum_{v \in V} f(v, u) \right) = 0
```

根据$$|f|$$的定义
```math
\displaystyle
|f| = \sum_{v \in V}f(s, v) - \sum_{v \in V}f(v, s) + \sum_{u \in S - \{s\}} \left( \sum_{v \in V}f(u, v) - \sum_{v \in V}f(v, u) \right)
```
展开并且重新组合
```math
\displaystyle
|f| = \sum_{v \in V} \left( f(s, v) + \sum_{u \in S - \{s\}} f(u, v) \right) - \sum_{v \in V} \left( f(v, s) + \sum_{u \in S - \{s\}} f(v, u) \right) \\
= \sum_{v \in V}\sum_{u \in S}f(u, v) - \sum_{v \in V}\sum_{u \in S}f(v, u)
```

进一步，**拆点**，把$$v \in V$$拆成$$(v \in S) + (v \in T)$$
```math
\displaystyle
|f| = \sum_{v \in S}\sum_{u \in S} f(u, v) + \sum_{v \in T}\sum_{u \in S}f(u, v) - \sum_{v \in S}\sum_{u \in S}f(v, u) - \sum_{v \in T}\sum_{u \in S}f(v, u)
\\ = \sum_{v \in T}\sum_{u \in S}f(u, v) - \sum_{v \in T}\sum_{u \in S}f(v, u) + \left( \sum_{v \in S}\sum_{u \in S}f(u, v) - \sum_{v \in S}\sum_{u \in S}f(v, u) \right)
```
注意到括号中的求和项是一样的
```math
\displaystyle
|f| = \sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{u \in S} \sum_{v \in T} f(v, u) = f(S, T)
```

#### 推论
流网络$$G$$中的任意流$$f$$的值不能超过$$G$$的任意切割的**容量**
```math
\displaystyle
|f| = f(S, T) = \sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{u \in S} \sum_{v \in T} f(v, u) \\
\leqslant \sum_{u \in S} \sum_{v \in T} f(u, v) \leqslant \sum_{u \in S} \sum_{v \in T} c(u, v) = c(S, T)
```
**流网络中的最大流的值，实际上等于一个最小切割的容量**

## 最大流最小割定理
设$$f$$是流网络$$G = (V, E)$$中的一个流，源点是$$s$$，汇点是$$t$$，以下条件等价
1）$$f$$是$$G$$的一个最大流
2）残量网络$$G_f$$中不包括任何增广路径
3）$$|f| = c(S, T)$$，其中$$c(S, T)$$是流网络$$G$$的某个切割

> 证明如下

首先，$$(1) \Rightarrow (2)$$显然，因为如果有增广路径，$$|f| + |f_p|$$构成一个更大的流，与$$|f|$$是最大流矛盾

考虑$$(2) \Rightarrow (3)$$，残量网络$$G_f$$中不存在$$s \to t$$的路径，采用反证法
不妨令$$S = \\{v \in V: v \in G_f,\text{ 并且从 s 处可达} \\}, T = V - S$$

显然我们有$$s \in S, t \notin S$$，划分$$(S, T)$$可以作为流网络$$G$$的一个切割
那么存在$$(u, v) \in E, (u, v) \notin E_f$$，也就是说$$c_f(u, v) = 0$$

而我们根据残量网络的定义，对于$$(u, v) \in E$$，$$c_f(u, v) = c(u, v) - f(u, v)$$，那么$$c_f(u, v) = 0$$
从而我们有$$f(u, v) = c(u, v), \Rightarrow f(v, u) = 0$$

根据切割的流量定义，我们有
```math
\displaystyle
f(S, T) = \sum_{u \in S}\sum_{v \in T}f(u, v) - \sum_{v \in T}\sum_{u \in S} f(v, u) = \sum_{u \in S}\sum_{v \in T}c(u, v) - \sum_{v \in T}\sum_{u \in S} 0 = c(S, T)
```
证明完毕

最后，$$(3) \Rightarrow (1)$$显然
因为$$|f| \leqslant c(S, T)$$，$$|f| = c(S, T)$$取到最大值

## 最大流一般算法
### Ford-Fulkerson 算法
1）初始化$$|f| = 0$$
2）**while** 在$$G_f$$中存在一条$$s \to t$$的增广路径$$p$$，那么
- 令$$c_f(p) = \min\\{c_f(u, v), \quad (u, v) \in p\\}$$

- **for** 所有$$(u, v) \in p$$
  如果是正向边，$$f(u, v) += c_f(p)$$，否则$$f(u, v) -= c_f(p)$$
  
算法执行的时候，最多需要增广$$|f|$$次，复杂度是$$O(E|f|)$$

### Edmonds-Karp 算法
1）定义每条边的权重为单位距离，$$\delta_f(u, v)$$表示残量网络$$G_f$$中$$s \to t$$的最短距离
2）沿着 **bfs** 找增广路径，选择$$s \to t$$的最短路作为增广路

> 时间复杂度分析

**引理** EK 算法运行在流网络$$G$$上，对于所有节点$$v \in V - \\{s, t\\}$$，残量网络$$G_f$$的最短路径$$\delta_f(s, v)$$
随着流量递增而单调增加

证明如下
反证法，假设$$|f| < |f'|$$，但是对于边$$(u, v)$$，我们却有$$\delta\_f(s, u) \leqslant \delta\_{f'}(s, u),  \ \delta\_f(s, v) > \delta\_{f'}(s, v)$$

首先，对于$$(u, v) \in E\_{f'}$$，那么一定有$$(u, v) \notin E_f$$，否则的话
```math
\delta_f(s, v) \leqslant \delta_f(s, u) + 1 \leqslant \delta_{f'}(s, u) + 1 = \delta_f'(s, v)
```
这与归纳假设矛盾

其次，$$(u, v) \in E\_f, (u, v) \notin E\_{f'}$$，这意味着操作增加了反向边$$v \to u$$的流量
即算法最后走的是$$E\_f(v, u)$$
```math
\delta_f(s, v) = \delta_f(s, u) - 1 \leqslant \delta_{f'}(s, u) - 1 = \delta_{f'}(s, v) - 2
```
这与$$\delta\_{f'}(s, v) < \delta\_f(s, v)$$矛盾

**定理**
Edmonds-Karp 算法执行的流量增广操作总次数是$$O(VE)$$
在残量网络$$G_f$$中，对于增广路径$$p$$，如果$$c_f(p) = c_f(u, v)$$，那么认为$$(u, v)$$是增广路径的关键边
对于$$|E|$$中的每条边而言，成为关键边的次数最多为$$|V|/2$$次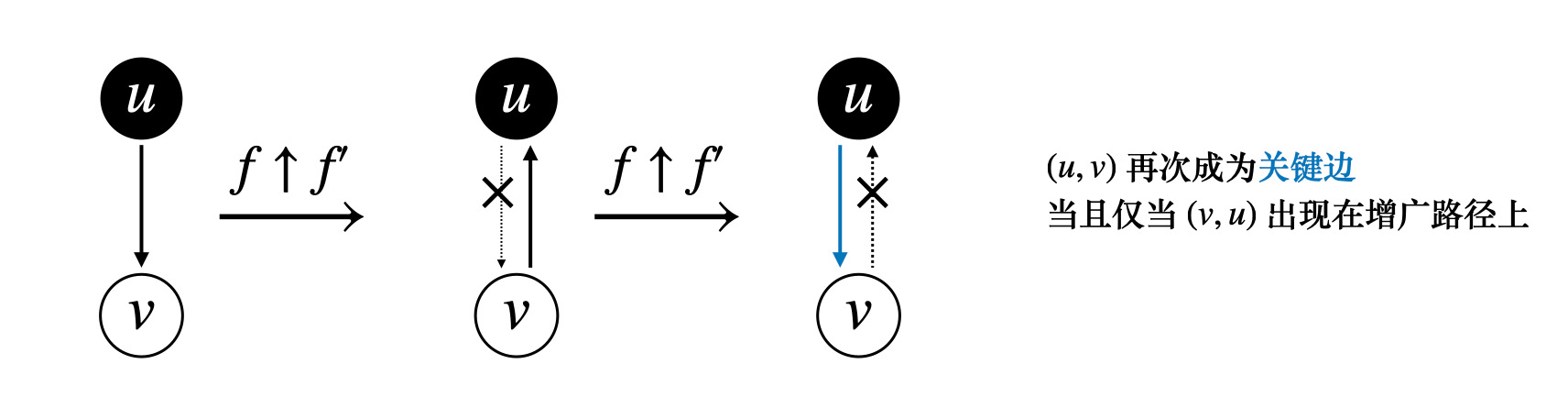

![](/media/content_img/flow04.jpg)

这里应用反向边这个概念，反向边就相当于我们**反悔，撤销之前的操作**
注意到，沿着增广路径增加流，关键边从残量网络$$G_f$$中消失，它什么时候再次成为关键边呢？
也就是说存在反悔行为，当$$(u, v)$$网络流量减小，$$(v, u)$$出现在增广路径上的时候

那么我们有
```math
\delta_f(s, v) = \delta_f(s, u) + 1 \\
\delta_{f'}(s, u) = \delta_{f'}(s, v) + 1
```
考虑一次增广，$$|f| < |f'|$$，我们有$$\delta\_{f}(s, v) \leqslant \delta\_{f'}(s, v)$$
```math
\delta_{f'}(s, u) = \delta_{f'}(s, v) + 1 = \delta_f(s, u) + 2
```
也就是说，一次增广，$$s \to ui$$的距离至少增加两个单位，而二者之间最大距离就是$$O(|V|)$$
所以$$(u, v)$$能够成为关键边$$O(|V|/2)$$次，关键边总数是$$O(|E||V|/2)$$

## Dinic 多路增广算法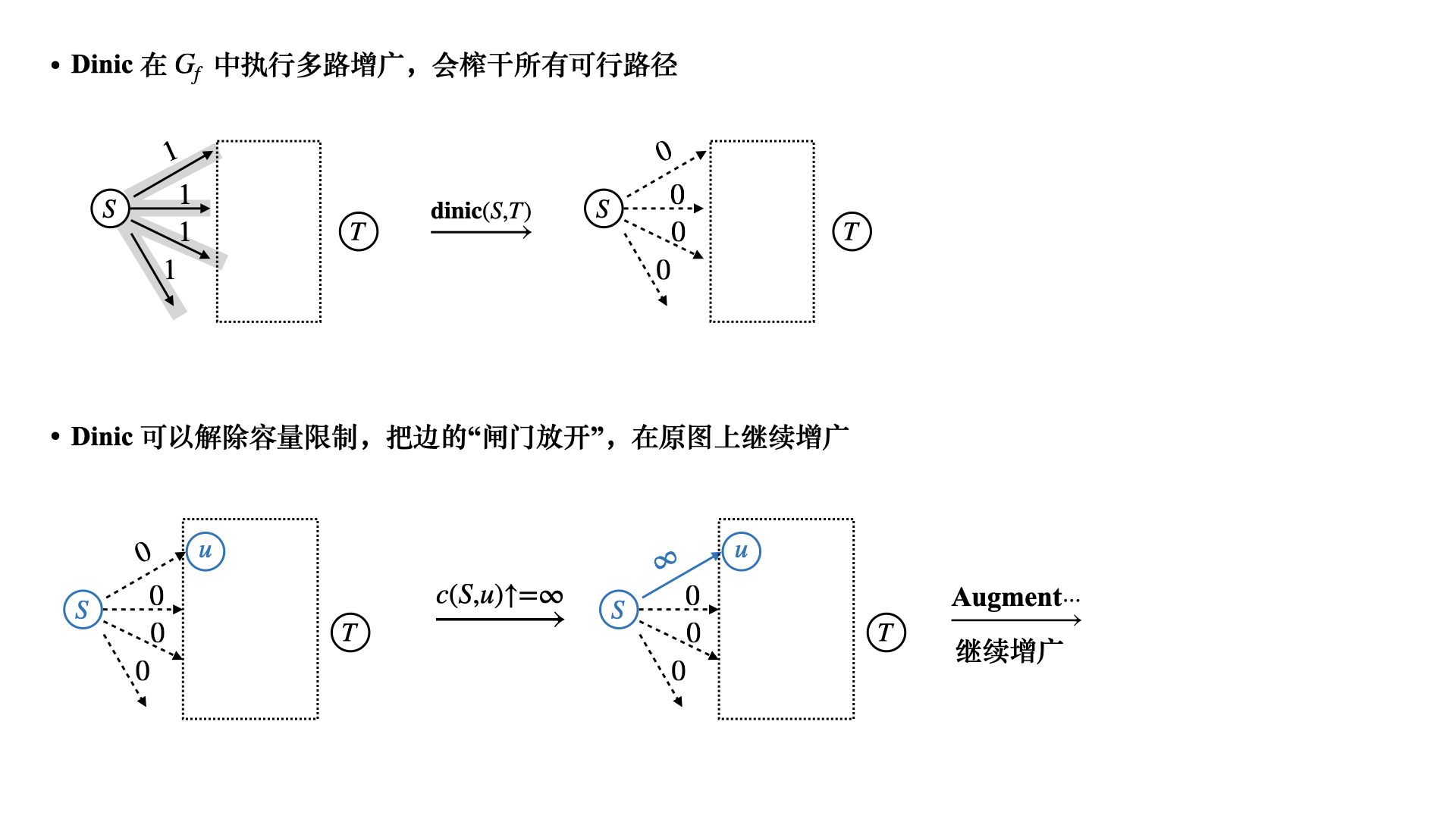
![](/media/content_img/flow05.jpg)
![](/media/content_img/flow06.jpg)

### Dinic 算法思想
1）沿着 bfs 最短路增广，通过 bfs 构造分层图，同时求出距离编号
注意，增广的时候，**有流量的正向边**我们才流过去，也就是说`if (e.flow and v 距离编号还没有求出来过)`
这个时候才进行增广，如果没有找到汇点，那么就意味着不存在增广路，`return false`

2）每找一轮，分层图可能因为反向边的加入，使得$$s \to t$$的距离变得更长，再继续找，直到没有增广路径
每找一轮，$$flow += \text{dfs}(s, +\infty)$$
```bash
while (bfs()) flow += dfs(s, numeric_limits<T>::max())
```

#### dfs 多路增广
对于每个点$$u$$有一个流量上限，比如$$(u, \lim)$$，一开始的时候，起点流量无穷大，$$(s, +\infty)$$
增广的过程大致如下
![](/media/content_img/flow07.png)

三个优化
1）当前弧优化，把增广完的分支及时删掉
2）流量上限优化，如果`lim = 0`，是不会再进行增广了，及时 break
3）零流优化，如果当前节点`flow = 0`，就说明流不出去了
之前我们分析，沿着 bfs 最短路增广，有势能$$(u, v): \delta_f(v) = \delta_f(u) + 1$$
而流不出去了，需要把$$\delta = -1$$，`dis(u) = -1`表示之后不会往这里流了

主算法的实现并不复杂
1）从当前弧开始，分别考虑每一个分支
2）考虑能不能增广？充要条件有两个，$$e.flow > 0$$并且分层图上，$$\delta_v = \delta_u + 1$$
然后`|f| = dfs(v, min(e.flow, lim))`， 增广`|f|`的流量
注意上面三个优化即可

### dinic 算法实现
```bash
template<class T> class maxflow {
public:
    struct _Edge {
        int to;
        T cap;
        _Edge(int to, T cap) : to(to), cap(cap) {}
    };
    int _n;
    vector<_Edge> e;
    vector<vector<int> > g;
    vector<int> cur, dis;

maxflow() {}
    maxflow(int n) {
        init(n);
    }
    void init(int n) {
        this->_n = n;
        e.clear();
        g.assign(n+5, {});
        cur.resize(n+5);
        dis.resize(n+5);
    }
    void addEdge(int u, int v, T cap) {
        g[u].push_back(e.size());
        e.emplace_back(v, cap);
        g[v].push_back(e.size());
        e.emplace_back(u, 0);
    }

bool bfs(int s, int t) {
        dis.assign(_n+5, -1);
        cur.assign(_n+5, 0);

queue<int> que;
        dis[s] = 0;
        que.push(s);

while (!que.empty()) {
            const int u = que.front(); que.pop();
            for (int i : g[u]) {
                auto [v, cap] = e[i];
                if (cap > 0 && dis[v] == -1) {
                    dis[v] = dis[u] + 1;
                    if (v == t) return true;

que.push(v);
                }
            }
        }
        return false;
    }

T dfs(int u, int t, T flow) {
        if (u == t) return flow;

auto rem = flow;

for (int &i = cur[u]; i < (int)g[u].size(); i++) {
            const int j = g[u][i];
            auto [v, cap] = e[j];

if (cap > 0 && dis[v] == dis[u] + 1) {
                auto f = dfs(v, t, min(rem, cap));
                e[j].cap -= f;
                e[j ^ 1].cap += f;
                rem -= f;

if (rem == 0) return flow;
            }
        }

return flow - rem;
    }

T dinic(int s, int t) {
        T flow = 0;
        while (bfs(s, t)) flow += dfs(s, t, numeric_limits<T>::max());
        return flow;
    }

struct Edge {
        int from, to;
        T cap, flow;
    };
    vector<Edge> edges() {
        vector<Edge> a;
        for (int i = 0; i < e.size(); i += 2) {
            Edge x;
            x.from = e[i + 1].to, x.to = e[i].to;
            x.cap = e[i].cap + e[i + 1].cap;
            x.flow = e[i + 1].cap;

a.push_back(x);
        }
        return a;
    }
};
```

上一篇：积性函数，莫比乌斯反演（二）下一篇：2024年12月一些算法比赛（一）

看完文章有啥想法