支配集，支配集常见的结论

[[ slider_text ]]

[[ item.c ]]

支配集，支配集常见的结论

发布时间 2025-01-03 作者：zhangminchen 来源：算法小站

图论

## 支配集的一些结论
### 支配集的直观概念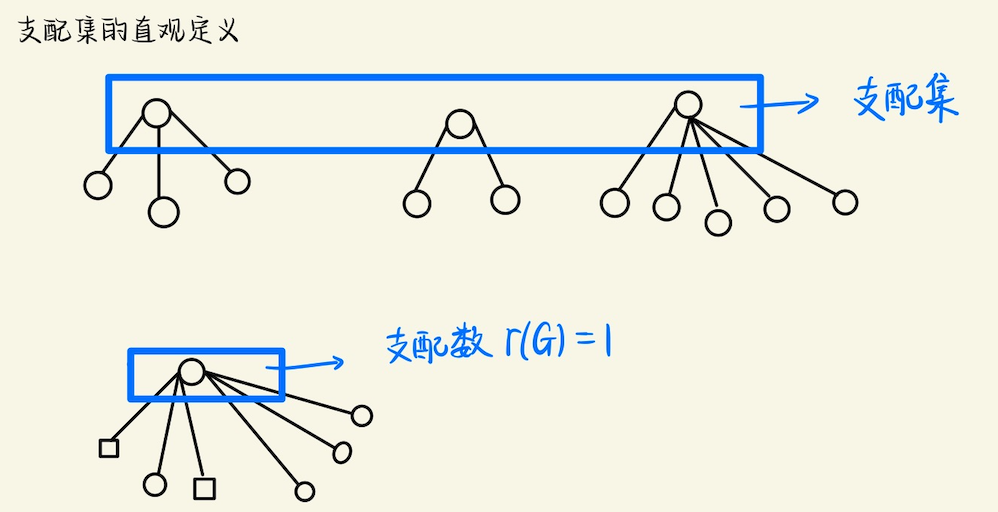
![](/media/content_img/domain01.png)

### 支配集的一些问题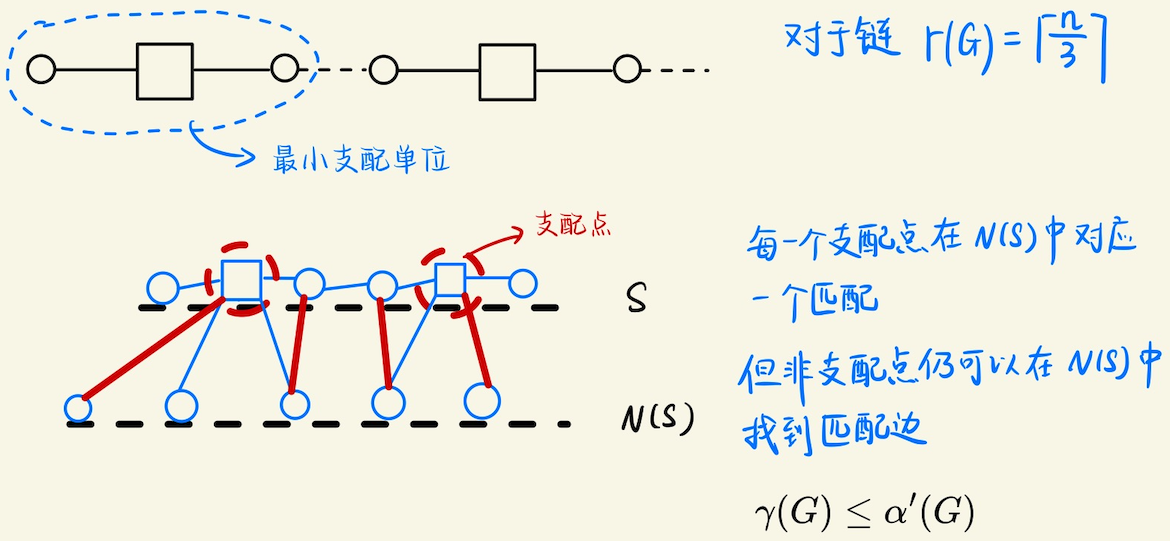

![](/media/content_img/domain02.png)

> 找出支配数和顶点覆盖数不相等的最小树

实际上，$$\gamma(G) = \lceil n/3 \rceil, \beta(G) = \lceil n / 2 \rceil$$，找到一条大小为$$6$$的链（路径）
满足支配数和顶点覆盖不等的最小树，就是$$P_6$$

> 求$$\gamma(C_n)$$和$$\gamma(P_n)$$的公式

和图中分析的一样，最小支配单位是$$3$$，所以$$\gamma(C_n) = \lceil n / 3 \rceil$$

> 设$$G$$是一个没有孤立顶点的图，$$S$$是$$G$$中的一个极小支配集，证明$$\bar{S}$$也是一个支配集
得出结论$$\gamma(G) \leqslant n(G) / 2$$

根据支配集定义，$$\forall x \notin S$$均有$$N(x) \in S$$，将$$x \leftrightarrow N(x)$$也成立
所以$$\bar{S}$$也是一个支配集，从而$$S \leqslant \dfrac{n(G)}{2}$$

> 证明，如果$$G$$是一个没有孤立顶点的$$n-$$顶点图，那么$$\gamma(G) \leqslant n - \beta^{\prime}(G) \leqslant n/2$$
对$$1 \leqslant k \leqslant n / 2$$构造一个满足$$\gamma(G) = k$$的连通$$n-$$顶点图$$G$$

对于第一部分，实际上$$\gamma(G) \leqslant \alpha^{\prime}(G) \leqslant n / 2$$成立（见图）
考虑构造，不难，只需要选出一个支配点，保证它的$$deg = \lfloor n / k \rfloor$$，然后再组合起来即可

> 设$$G$$是一个$$n-$$顶点简单图，证明

> a) $$\lceil \dfrac{n}{1+\Delta(G)} \rceil \leqslant \gamma(G) \leqslant n - \Delta(G)$$

> b) $$(1 + diam(G)) / 3 \leqslant \gamma(G) \leqslant n - \lceil (2diam(G)) / 3 \rceil$$
注$$diam$$指的是直径

考虑证明a)，对于支配点$$s$$，支配单位$$= |\\{s\\} \cup \\{N(S)\\}|\_{\max} = (1 + \Delta(G))$$
从而$$\lceil \dfrac{n}{1+\Delta(G)} \rceil \leqslant \gamma(G)$$

另一方面，取度数最大的点$$s$$，那么最坏情况，$$\Delta(G)$$个点不被选中，而$$s$$被选到支配集中
这样支配集大小的上界就是$$n - \Delta(G)$$

考虑证明b），最长路径的长度实际上就是$$\text{diam}(G)$$，有点$$1 + \text{diam}(G)$$个
根据前面的结论，$$\gamma(G) \geqslant (1 + diam(G)) / 3$$

考虑$$\gamma(G)$$的上界，需要考虑**最少的，不需要放入支配集的，非支配点有几个**？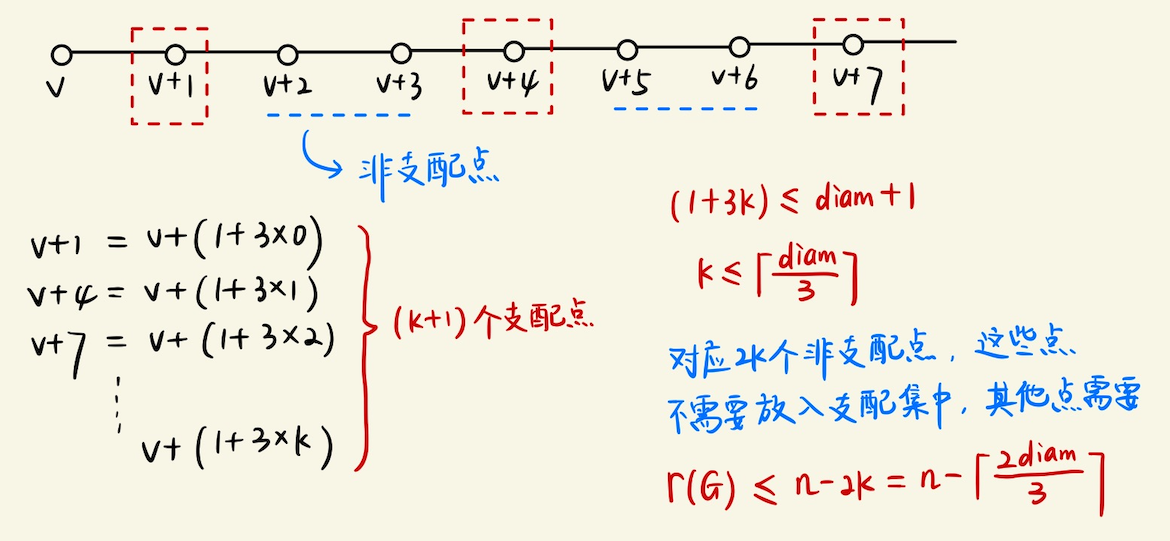
![](/media/content_img/domain03.png)

> 证明，如果$$G$$的直径至少是$$3$$，那么$$\gamma(\bar{G}) \leqslant 2$$

其实并不难，可以找到$$\\{u, v\\}$$，使得$$d(u, v) = 3$$，这样把$$G$$分成两部分
分别是$$\\{u \to v\\} \cup \\{G - (u \to v)\\}$$，这样$$\bar{G} = \\{u \to v\\}$$
最多仅需要$$u, v$$两个点，即可支配$$\bar{G}$$，从而$$\gamma(\bar{G}) \leqslant 2$$

> 对所有的$$k \in \mathbb{N}$$，构造一个支配数为$$2k$$的$$5k-$$顶点连通图，构造一个满足$$\gamma(G) = 3n(G) / 8$$的$$3-$$正则图

![](/media/content_img/domain04.png)

> 在超立方体$$Q_4$$中，确定支配集，独立支配集，连通支配集和完全支配集的**最小大小**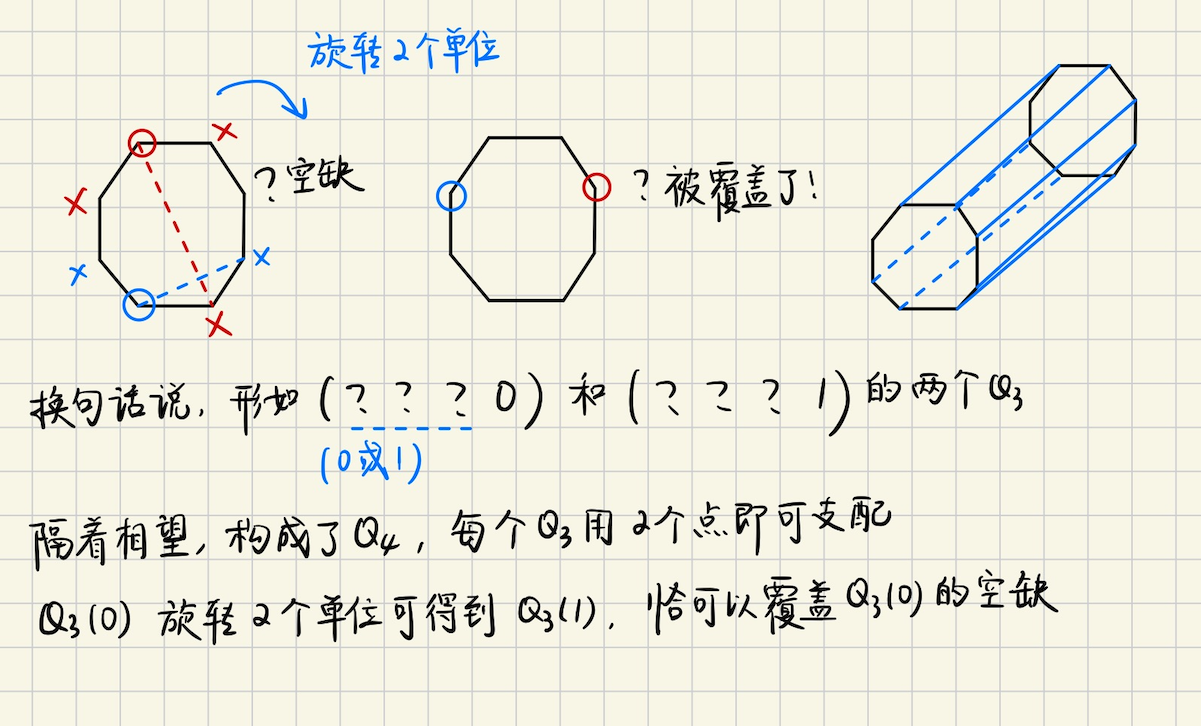

![](/media/content_img/domain05.png)

证明其实并不难，对于$$Q_4$$，是$$\displaystyle k = \binom{4}{1}$$的正则图
因为$$Q_4$$可以在$$4$$个位标处，任意一个位置取不同的值（剩下位标处值相同），这样就得到了一条边

另一方面，$$Q_4$$含有几个点呢？$$n(Q_4) = 2^4 = 16$$个点，同时又是一个$$k = 4$$的正则图
所以一个块有$$5$$个点，每个块都有一个**支配点**，支配集大小就看有几个这样的块？有$$\displaystyle \lceil \dfrac{16}{5} \rceil = 4$$
所以支配集，独立支配集，连通支配集，完全支配集的最小大小，都是$$4$$

> 在$$8 \times 8$$的棋盘上，找到一种放置$$5$$个皇后的方法，使得它们能够攻击所有方格中的对方
证明，没有一种放置方法能使这$$5$$个皇后之间不能互相攻击
皇后图的独立支配数，超过了它的支配数，这里的支配数是$$7$$

对于每一个皇后，看作一个**支配点**，所有**同列，同行，同对角线的格子**，都被其支配
![](/media/content_img/domain06.png)

实际上，$$11 \times 11$$也可以被$$5$$个皇后支配
![](/media/content_img/domain07.png)

一个猜想，对于$$x \times x$$的棋盘，$$k = \lceil \dfrac{x^2}{3x-2} \rceil + 1$$是不是足以支配整个棋盘？
支配的意思，就是放置了$$k$$个皇后之后，接下来不论怎么放皇后，都会被棋盘上已经存在的皇后攻击到

有意思的是，从支配集考虑，实际上每个皇后，能支配的点不会有$$3x-2$$那么多
![](/media/content_img/domain08.png)

> 对所有$$n \in \mathbb{N}(n \geqslant 4)$$，构造一个支配数为$$2$$的$$n-$$顶点树，使得其独立支配集的最小大小是$$\lfloor n / 2 \rfloor$$

![](/media/content_img/domain09.png)

> 证明，$$K(1, r)-$$无关图$$G$$有一个大小至多为$$(r-2)\gamma(G) - (r-3)(r \geqslant 3)$$的独立支配集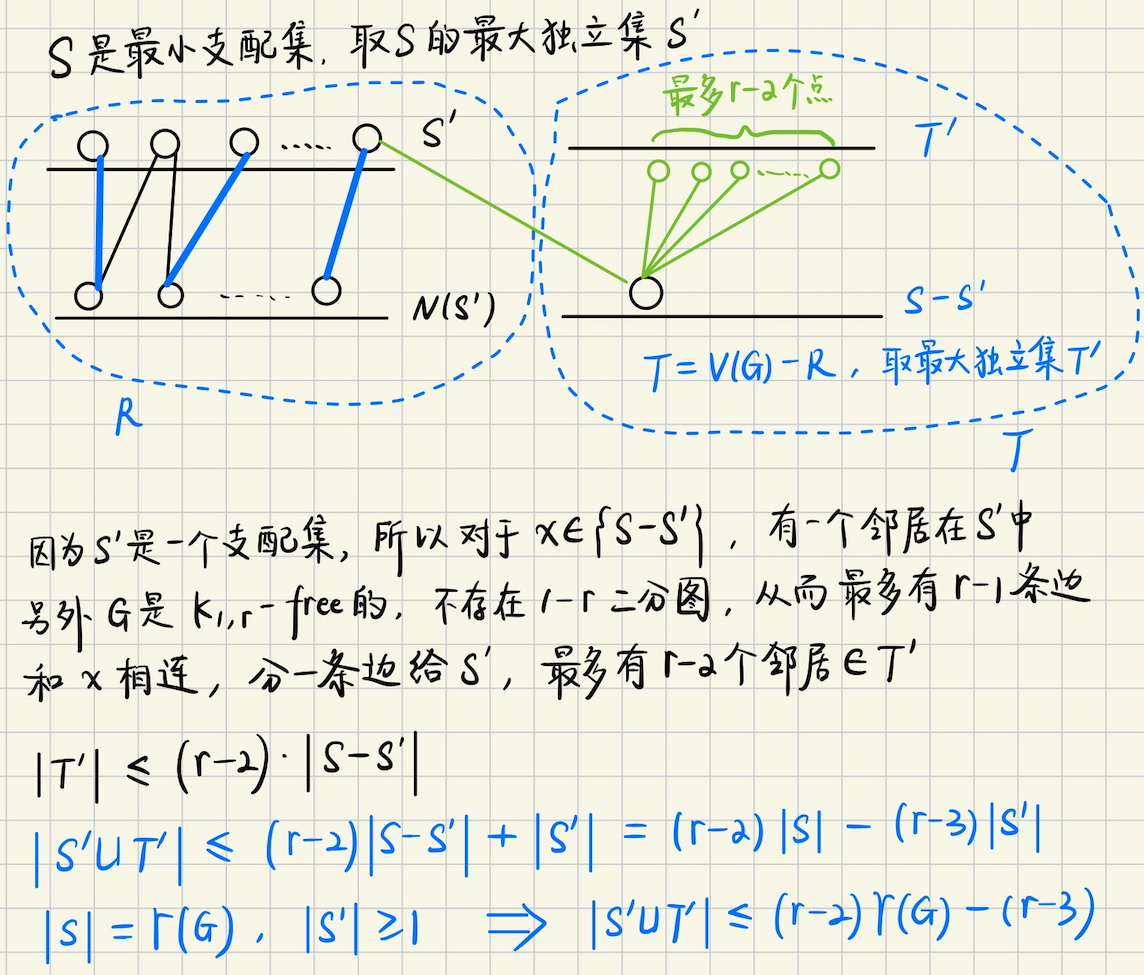

![](/media/content_img/domain10.png)

> 证明，在一个阶是$$n$$的一个连通图$$G$$中，连通支配集大小的最小值，等于$$n$$减去生成树中叶子的最大数目

阶，就是图顶点的个数
假设叶节点有$$l$$个，每一个叶子结点的父亲，都应该$$\in S$$，$$S$$是支配集
这样我们就有$$|S| = n - l$$

> 对$$k \leqslant 5$$，满足$$\delta(G) \geqslant k$$的任意图有一个大小至多为$$\dfrac{3n(G)}{k+1}$$的连通支配集
用下面的图，证明这个界几乎是最好的
将$$3m$$个两两不相交的团，排列成环状，并使得每个顶点，与该顶点之前的团，和之后的团中，任意顶点都相邻
令各个团的大小分别是$$\lceil k / 2 \rceil, \lfloor k / 2 \rfloor, 1, \lceil k / 2 \rceil, \lfloor k / 2 \rfloor, 1, \cdots$$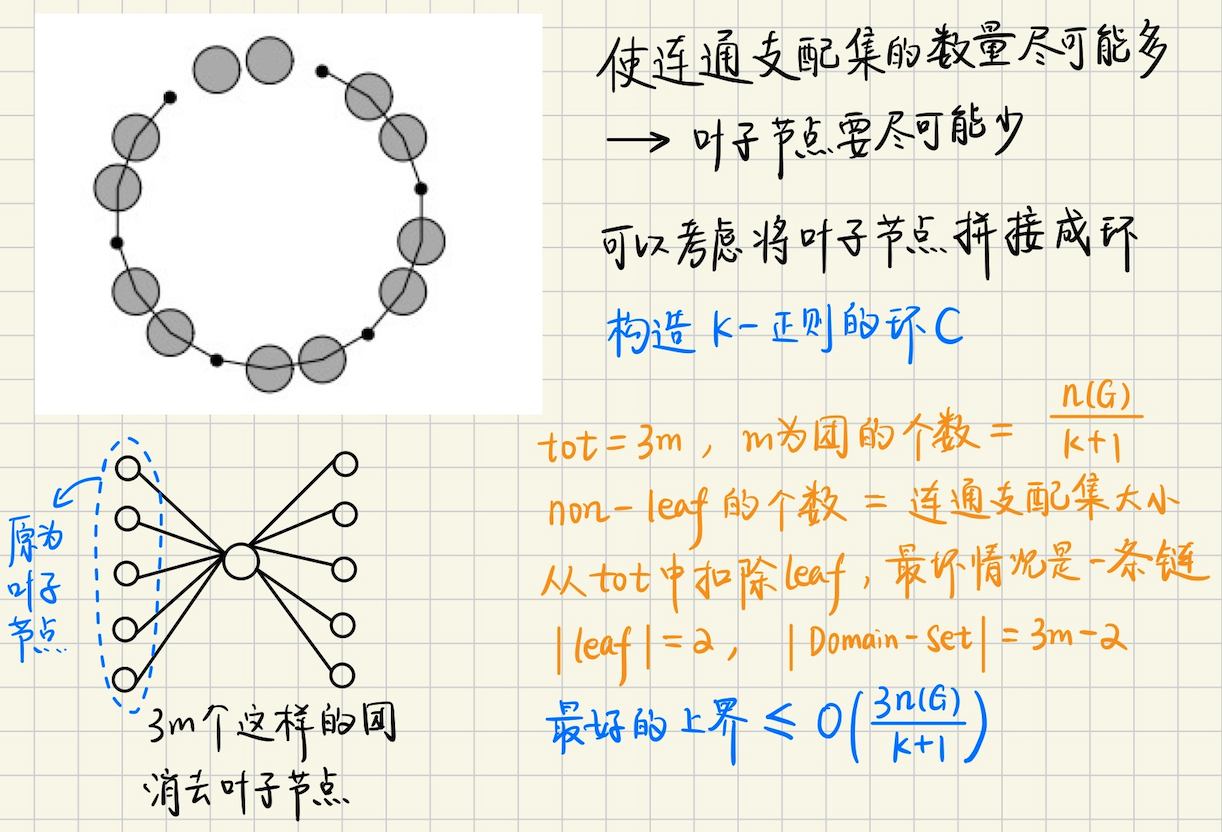

![](/media/content_img/domain11.png)

上一篇：二分图，匹配和因子已经是最后一篇啦

看完文章有啥想法