数位dp（一）

[[ slider_text ]]

[[ item.c ]]

发布时间 2024-05-28 作者：zhangminchen 来源：算法小站

数位dp 背包问题

## 数位 dp 概述
**问题描述**
请问$$[l, r]$$中有多少个数字$$a$$满足存在`3`个连续的数位$$a\_i, a\_{i+1}, a\_{i+2}$$使得$$a\_i < a\_{i+1} < a\_{i+2}$$
其中$$a_i$$表示$$a$$从左数到右第$$i$$位上的值

### 算法分析
这种问题一般都不会直接算$$[l, r]$$的答案，一般都是`solve(r) - solve(l-1)`
`solve(x)`计算$$[1 \cdots x]$$的答案

![](/media/content_img/digitdp-01-1.png)
![](/media/content_img/digitdp-01-2.png)

> 为什么需要`x += 1`，考虑每一位的时候，都会 for 到**当前这一位`-1, 即 d[i] - 1`**
只不过首位的时候是从`1`开始，`[1...d[0]-1]`，其他位是从`0`开始，`[0...d[i]-1]`

### 算法实现
```bash
// rem, 还剩多少位，exist 存不存在连续3位递增，last 末尾的数是多少，inc 末尾的递增长度
ll dp[20][2][10][5];

ll dfs(int rem, int exist, int last, int inc) {
    if (rem == 0) return 1LL * exist;

if (dp[rem][exist][last][inc] != -1) {
        return dp[rem][exist][last][inc];
    }

ll &ans = dp[rem][exist][last][inc];
    ans = 0;
    for (int x = 0; x <= 9; x++) {
        int inc_ = (x > last) ? min(inc+1, 3) : 1;
        ans += dfs(rem-1, exist | (inc_ == 3), x, inc_);
    }
    return ans;
}

ll solve(ll x) {
    x += 1;
    vector<int> d;
    while (x) d.push_back(x % 10), x /= 10;
    reverse(d.begin(), d.end());
    auto m = d.size();
    
    ll ans = 0;
    // [1-9], [10-99], [100-999]...
    for (int i = 1; i <= m-1; i++) {
        for (int j = 1; j <= 9; j++) ans += dfs(i-1, 0, j, 1);
    }

// [1?????....x]
    int exist = 0, last = 0, inc = 0;
    for (int i = 0; i < m; i++) {
        for (int j = (i == 0) ? 1 : 0; j < d[i]; j++) {
            int inc_ = (j > last) ? min(inc+1, 3) : 1;
            ans += dfs(m-1-i, exist | (inc_ == 3), j, inc_);
        }
        inc = (d[i] > last) ? min(inc+1, 3) : 1;
        exist |= (inc == 3);
        last = d[i];
    }

return ans;
}

int main() {
    memset(dp, -1, sizeof(dp));
    ll ans = solve(r) - solve(l-1);
}
```

## CF 739(Div 3) F.Nearest Beautiful Number
**问题描述**
**[F.Nearest Beautiful Number](https://codeforces.com/contest/1560/problem/F2)**
给你一个正整数$$n$$，找到一个$$\geqslant n$$的，最小的$$k$$美丽数$$x$$
一个数是$$k$$美丽的，当且仅当它的十进制中包含最多$$k$$个不同的数位

### 算法分析
这是一类问题，有一类问题是
找到`字典序 >= xxx...xx`的，第一个满足的数$$v$$，其中`xxx...xx`可能会很大，长度可能是$$10^5$$
![](/media/content_img/digitdp-02-1.png)
### 算法实现
```bash
void solve() {
    int n, k;
    scanf("%d%d", &n, &k);

vector<int> d;
    while (n) d.push_back(n % 10), n /= 10;
    reverse(d.begin(), d.end());

vector<int> vis(15, 0);

function<bool(int, bool, int, int)> dfs = [&]
    (int x, bool larger, int cnt, int num) -> bool {
        if (x == d.size()) {
            printf("%d\n", num);
            return true;
        }
        
        for (int i = larger ? 0 : d[x]; i <= 9; i++) {
            vis[i] += 1;

int ncnt = cnt;
            if (vis[i] == 1) ncnt += 1;
            if (ncnt <= k && dfs(x+1, larger | (i > d[x]), ncnt, num*10+i)) return true;
            vis[i] -= 1;
        }
        return false;
    };
    
    dfs(0, 0, 0, 0);
}
```
复杂度是正确的
![](/media/content_img/digitdp-02-2.png)

### 问题拓展
如果问**有至少$$k$$个不同的数位**，要怎么做呢？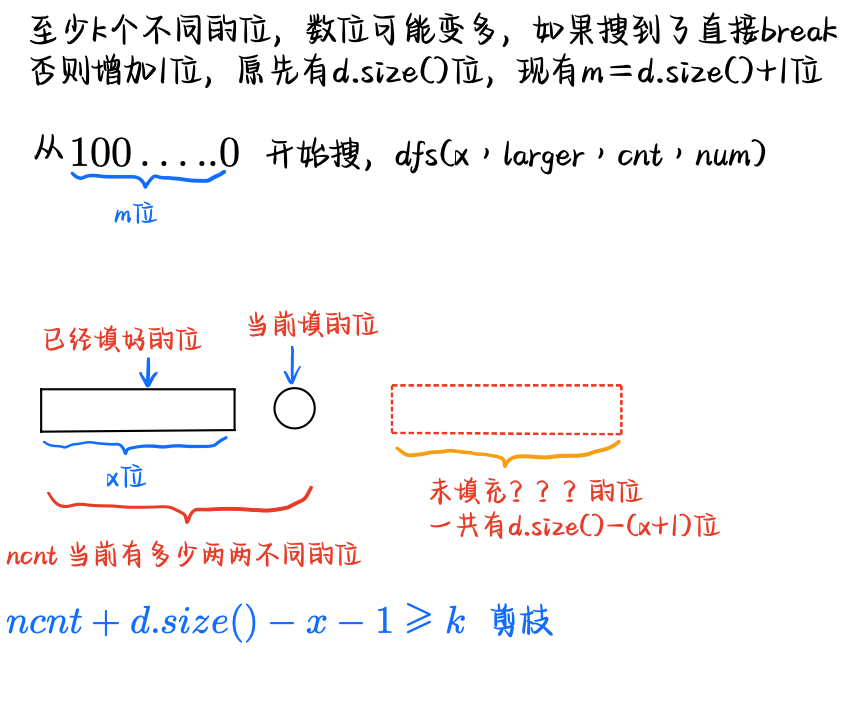
![](/media/content_img/digitdp-02-3.png)

这里剪枝的条件是，未填上的位，极端情况**可以都填上不同的数**

```bash
void solve() {
    int n, k;
    scanf("%d%d", &n, &k);

vector<int> d;
    while (n) d.push_back(n % 10), n /= 10;
    reverse(d.begin(), d.end());

vector<int> vis(15, 0);

int ncnt = cnt;
            if (vis[i] == 1) ncnt += 1;
            if (ncnt + d.size()-x-1 >= k && dfs(x+1, larger | (i > d[x]), ncnt, num*10+i)) return true;
            vis[i] -= 1;
        }
        return false;
    };
    
    while (true) {
        if (dfs(0, 0, 0, 0)) break;
        int m = d.size() + 1;
        d.clear();
        d.push_back(1);
        for (int i = 0; i < m-1; i++) d.push_back(0);
    }
}
```

## 梦幻岛宝珠
**问题描述**
**[梦幻岛宝珠](https://www.luogu.com.cn/problem/P3188)**
给定$$n$$个物品和背包的总容量$$W$$，每个物品有一个价值$$v$$和体积$$w$$，保证$$w = a \cdot 2^b(a \leqslant 10, b \leqslant 30)$$
求最大价值

### 算法分析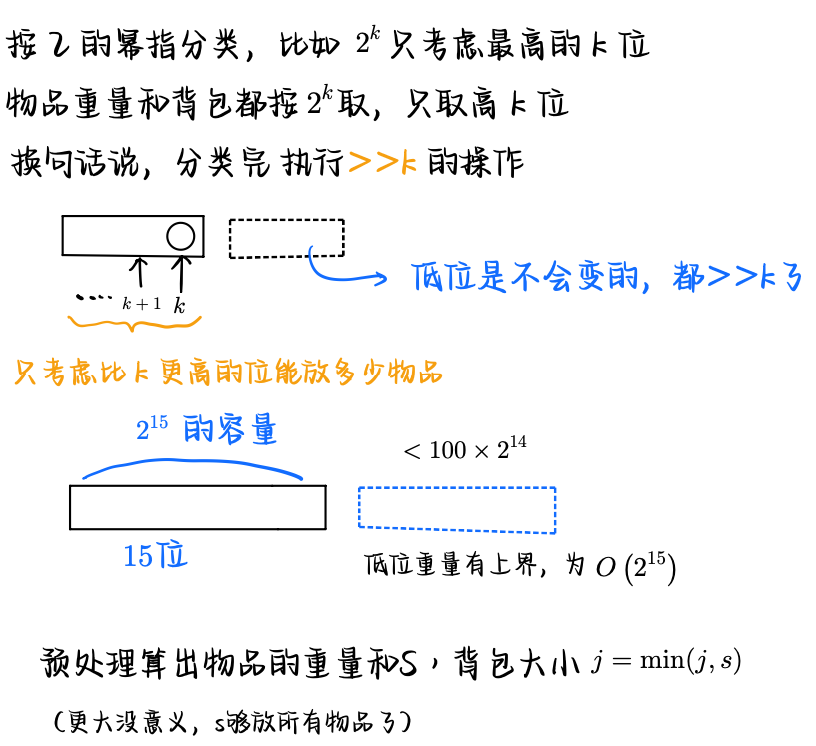
![](/media/content_img/digitdp-03-1.png)

> 注意开始的时候要先取关于容量$$j$$**的后缀最大值**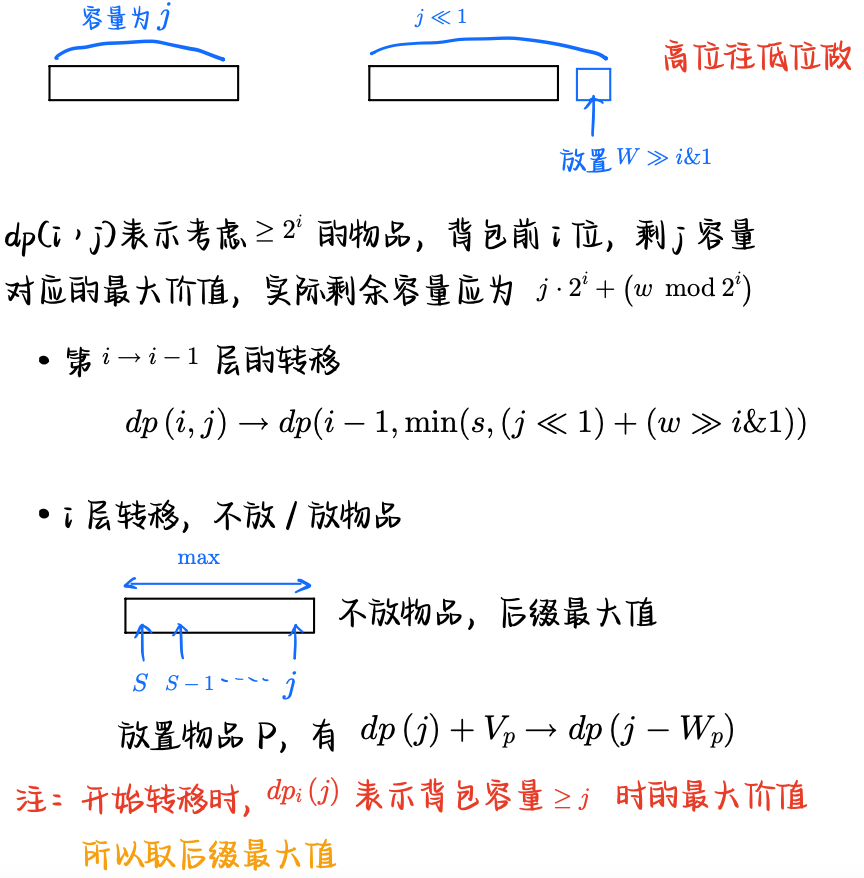

![](/media/content_img/digitdp-03-2.png)

### 算法实现
```bash
void solve() {
    vector<vector<PII> > item(35, vector<PII>());
    int s = 0;
    for (int i = 0; i < n; i++) {
        int w, v;
        scanf("%d%d", &w, &v);
        int lev = __builtin_ctz(w);
        w >>= lev, item[lev].push_back({w, v});
        s += w;
    }

vector<ll> dp(maxn, -inf), g(maxn, 0);
    dp[0] = 0;

for (int i = 30; i >= 0; i--) {
        for (int j = 0; j <= s; j++) g[j] = dp[j], dp[j] = -inf;
        for (int j = 0; j <= s; j++) {
            chmax( dp[min(s, (j<<1)+(W>>i&1))], g[j] );
        }

for (int j = s-1; j >= 0; j--) chmax(dp[j], dp[j+1]);
        for (auto p : item[i]) {
            auto vp = p.second, wp = p.first;
            for (int j = wp; j <= s; j++) chmax( dp[j-wp], dp[j]+1LL*vp );
        }
    }
    ll ans = dp[0];
    printf("%lld\n", ans);
}
```

### 01背包的另一种写法
**01 背包**问题，考虑第$$i$$个物品，选择**不放入**
也可以从**后缀最大值**的角度来考虑，表示背包**还剩下的容量**$$\geqslant j$$时候的最大价值
![](/media/content_img/digitdp-03-3.png)
```bash
int main() {
    freopen("input.txt", "r", stdin);
    int n, m;
    scanf("%d%d", &n, &m);

vector<PII> item(n+1, PII());
    for (int i = 1; i <= n; i++) {
        int vi, wi;
        scanf("%d%d", &vi, &wi);
        item[i] = PII(vi, wi);
    }

vector<ll> dp(maxn, -inf), g(maxn, 0);
    dp[0] = 0;
    for (int i = 1; i <= n; i++) {
        auto [vi, wi] = item[i];

for (int j = 0; j <= m; j++) g[j] = dp[j], dp[j] = 0;
        for (int j = m-1; j >= 0; j--) chmax(dp[j], max(g[j], g[j+1]));
        for (int j = vi; j <= m; j++) chmax(dp[j-vi], dp[j] + wi);
    }

ll ans = dp[0];
    printf("%lld\n", ans);
}
```

上一篇：树形dp在算法竞赛中的应用下一篇：数位dp（二）

看完文章有啥想法