数位dp（二）

[[ slider_text ]]

[[ item.c ]]

发布时间 2024-06-13 作者：zhangminchen 来源：算法小站

数位dp

## 数位 dp 解决乘法问题
**问题描述**
**[快速乘法](http://hihocoder.com/contest/challenge29/problem/2)**
将$$x \times a$$替换成若干个二进制幂的混合运算
$$(x \ll a_0) op_1(x \ll a_1) op_2 (x \ll a_2) \cdots op_n(x \ll a_n)$$，$$op$$是`+ 或者 -`
`移位，+，-`三种运算都需要一个单位的时间，现在给定$$a$$的二进制形式
求实现$$x \times a$$**最少**需要多少单位的时间

### 算法分析
![](/media/content_img/digitdp2-01-1.png)
根据以上分析，这启发我们根据**数位 dp**来设计算法
一看上去好像很难做，题目的意思是，通过若干次**右移操作的复合**，从`0`构造出$$x \times a$$
那我们可以反过来，考虑若干次**左移操作的复合**，将`x`变成`0`

![](/media/content_img/digitdp2-01-2.png)
### 算法实现
```bash
int main() {
	// 以字符串形式输入数，省略输入
	
    vector<int> dp(maxn, inf);
    dp[0] = 0;

vector<int> s(maxn, 0);
    for (int i = 1; i <= n; i++) s[i] = s[i-1] + (str[i] == '0');
    
    int j = -1;
    for (int i = 1; i <= n; i++) {
        if (str[i] == '0') {
            chmin(dp[i], dp[i-1]);
        }
        else {
            chmin(dp[i], dp[i-1] + 1);
            if (j-1 >= 0) chmin(dp[i], dp[j-1] + s[i] - s[j-1] + 2);

if (j == -1 ||
                dp[i-1]+s[i+1]-s[i-1]+2 <= dp[j-1]+s[i+1]-s[j-1]+2) j = i;
        }
    }
    int ans = dp[n]*2 - 1;
    printf("%d\n", ans);
}
```
### 算法分析二
对$$a$$**按位来考虑**，$$x \times a$$会发生什么呢？$$x \times (a_02^0 + a_12^1 + \cdots + a_i2^i + \cdots a_n2^n)$$，其中$$a_i = \\{0, 1\\}$$

从低位到高位来考虑，每一次操作，$$i-1 \to i$$我们可能需要引入**额外的$$1$$**
1）如果$$a_i = 0$$，这一位不计贡献，转移不需要额外代价
2）如果$$a_i = 1$$，那么在$$i$$位引入`1`的同时，不破坏其他位，通过右移和加法，怎么做呢？
不难想到是形如`+ (100...00)`，那么这个`100...0`怎么来呢？
第一是在考虑低位的时候，就构造了`100...0`，直接移位可以得到
第二，就是把低位的一段先全部改成`11...1`，改哪一段呢？不知道，先枚举
不妨设改了`[j...i]`这一段，都改成`1`，这需要代价，这部分代价就是这一段`0`的个数
然后低位`[1...j-1]`实际上有形如`100...0`的数，分别移位到`i+1, j`，然后$$- (2^{i+1} - 2^{j})$$

这样我们记$$dp(i)$$表示考虑低`[1...i]`位，且这些位中存在（或可以构造）形如`100...0`的数
最小的修改代价
那么就有转移
```math
\displaystyle
dp(i) = \min_{j \in [1\cdots i-1]} dp(j-1) +(\text{[j, i] 全部改成 1 的代价}) + 2
```
最后的$$2$$，实际上是因为$$[1\cdots j-1]$$的`100..0`要移位`2`次做减法
一次是到`i+1`位，一次是到`j`位，这样才能够使得`[j, i]`这一段都是`1`
另外，很显然`[j, i]`全部改成`1`，那么至少要有`2`位，也就是$$j \leqslant i-1$$

### 算法实现二
这个化简就非常常见了，分离$$i, j$$
```math
\displaystyle
dp(i) = cnt(i) + 2 + \min_{1 \leqslant j \leqslant i-1} (dp(j-1) - cnt(j-1)) 
```
其中$$\min$$的部分用前缀最小值`dpv`维护，算完`dp(i)`之后，令`chmin(dpv, dp(i-1) - cnt(i-1))`

```bash
int main() {
	// 省略多余代码
    vector<int> cnt(n+1, 0);
    for (int i = 1; i <= n; i++) cnt[i] = cnt[i-1] + (str[i] == '0' ? 1 : 0);

vector<int> dp(n+5, inf);
    dp[0] = 0;

int dpv = inf;
    for (int i = 1; i <= n; i++) {
        if (str[i] == '0') chmin(dp[i], dp[i-1]);
        else {
            chmin(dp[i], dp[i-1] + 1);
            chmin(dp[i], cnt[i] + 2 + dpv);
        }
        chmin(dpv, dp[i-1] - cnt[i-1]);
    }
    auto ans = dp[n] * 2 - 1;
}
```

## CCPC Changchun 2020 D
**[CCPC Changchun 2020 D. Meaningless Sequence](https://codeforces.com/gym/102832/problem/D)**
**问题描述**
`cnt(n)`表示`n`的二进制中`1`的个数，$$a_n = c^{cnt(n)}$$

求$$\sum_{i = 0}^{n} a_i$$，其中$$n$$按二进制给出，不超过$$2^{3000}$$

### 算法分析

原题意给出 $$a\_{n} = c \cdot \max\_{0\leqslant i < n} a\_{n \textbf{ and } i}$$，要先考虑一下$$a_n$$等于多少

> **这种题目怎么做呢？**先打表，不妨取$$c = 2, 3$$等几种情况，然后再找规律
不难发现，打表之后，我们有$$n = 15$$，答案是$$3^4$$，$$n = 16$$，答案居然是$$3^1$$
这样就可以找规律了

规律不难找。因为$$i \textbf{ and } j$$操作，会让$$i$$变小
如果$$i$$的某一位`?`是$$0$$，它不会变出$$1$$，也就是说，考虑`a[ i & j ]`，第`?`位对答案$$ans_i$$没有贡献
假设`i`形如`100..11..01`，因为$$i \textbf{ and } j$$，$$j < i$$，我们是一定要舍弃一个数位上的`1`的
从低位到高位来看，最高位加入`1`，那么$$i$$二进制关于`1`的个数`+1`
那么我们应该**尽可能保住低位全部的 1**，舍去高位的那个`1`，这样是最划算的

![](/media/content_img/digitdp2-02-1.png)

实际上就是看**有几个满足条件的数**，对答案的贡献就是多少
![](/media/content_img/digitdp2-02-2.png)

### 算法实现
```bash
int main() {
    freopen("input.txt", "r", stdin);
    string str;
    int c;
    cin >> str >> c;

int n = str.size();
    vector<mint> pw(maxn, 0);
    pw[0] = 1;
    for (int i = 1; i <= n; i++) pw[i] = pw[i-1] * mint(c+1);

mint ans = 0, pre = 1;
    for (int i = 0; i < n; i++) {
        if (str[i] == '1') {
            ans += pre * pw[n-1-i];
            pre *= mint(c);
        }
    }
    ans += pre;
    printf("%d\n", ans.val());
}
```

> 总结，数位 dp 的思路，遇到比如说$$\leqslant n$$的数，满足条件的有多少个之类的
按数位，对$$n$$从**高位到低位**考虑，比如当前考虑到前缀`i`这个位置
决策一，填上`[0...d(i)-1]`，那么**低位**`[i+1...n]`可以随便填，随便填的时候，有时候常用**二项式定理**来做统计
决策二，填上`d(i)`，接下来`i = i+1`接着 dp 下一位

计算$$\sum_i c^{\text{popcount(i)}}$$还有一种数位`dp`的方法
```bash
void solve() {
    auto dfs = [&](auto &dfs, int i, int smaller) -> mint {
        mint &ans = dp[i][smaller];
        if (i > n) {
            return ans = mint(1);
        }
        if (dp[i][smaller].val() > 0) return dp[i][smaller];

mint res = 0;

int hi = ( (smaller || str[i] == '1') ? 1 : 0 );
        for (int j = 0; j <= hi; j++) {
            if (j == 0) res += dfs(dfs, i+1, smaller | (j < hi));
            else res += mint(c) * dfs(dfs, i+1, smaller | (j < hi));
        }

return ans = res;
    };

auto ans = dfs(dfs, 1, 0);
    printf("%d\n", ans.val());
}
```

## CCPC Jinan 2020
**[CCPC Jinan 2020 L. Bit Sequence](https://ac.nowcoder.com/acm/contest/10662/L)**
**问题描述**
令$$f(x)$$表示$$x$$二进制表示中$$1$$的个数
现在给你一个序列$$a\_0, a\_1, \cdots, a\_{m-1}$$，问你有多少个数$$x \in [0, L]$$满足
$$\forall i \in [0, m-1], f(x+i) \bmod 2 = a\_i$$

### 算法分析
先翻译一下题目讲什么事情，给你一些数`a[0], a[1], ..., a[m-1]`，对应成一个**无穷序列**
`0 1 1 0 1 0 0 1 0 1 1 0 ....`，每一个`0/1`表示$$a_i$$二进制中`1`的个数的**奇偶性**
然后给你一段值，`x+i = 0 1 0 0`，问这段值在满足$$x \leqslant [0, L]$$的条件下，**出现了几次**

>  这是一个 Thue-Morse 序列，只需要关心 1 出现的次数的奇偶性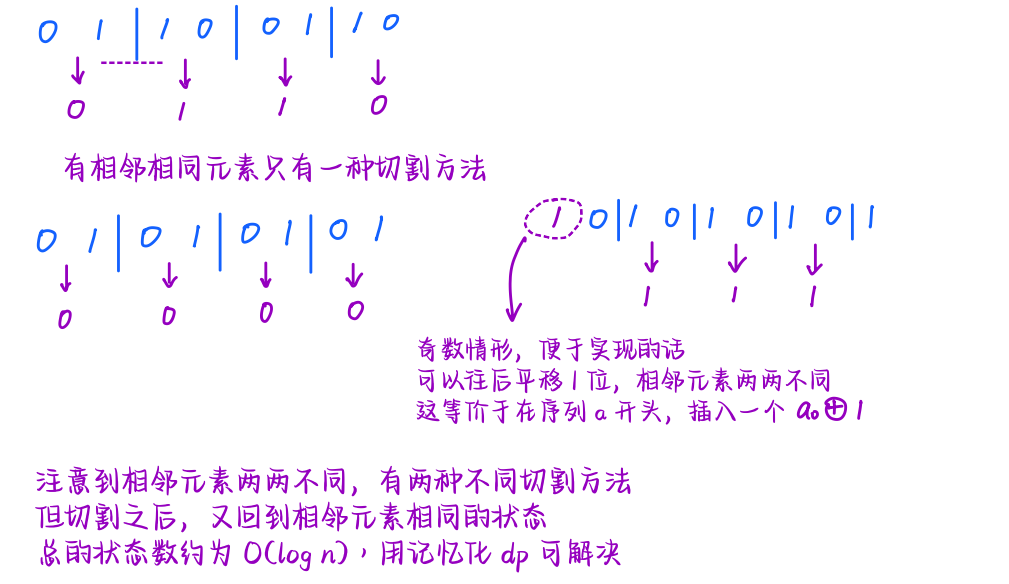

![](/media/content_img/digitdp2-03-1.png)
![](/media/content_img/digitdp2-03-2.png)
![](/media/content_img/digitdp2-03-3.png)
![](/media/content_img/digitdp2-03-4.png)

### 算法实现
```bash
typedef pair<ll, vector<int> > PII;

void solve() {
    int m;
    ll L;
    scanf("%d%lld", &m, &L);
    vector<int> a(m, 0);
    for (int i = 0; i < m; i++) scanf("%d", &a[i]);

function<vector<int>(vector<int>)> reduce = [&](vector<int> a) -> vector<int> {
        vector<int> b;
        for (int i = 0; i < a.size(); i += 2) {
            b.push_back(a[i]);
            if (i+1 < a.size() && a[i] == a[i+1]) return vector<int> (0);
        } 
        return b;
    };

// dp memory
    map<pair<ll, vector<int> >, ll> dp;

function< ll(ll, vector<int> ) > calc = [&](ll L, vector<int> a) -> ll {
        if (a.empty()) return 0;
        if (dp.count(PII( L, a ))) return dp[ PII(L, a) ];

if (L <= 0) {
            ll res = 1;
            for (int i = 0; i < a.size(); i++) {
                if (__builtin_parity(i) != a[i]) {
                    res = 0;
                    break;
                }
            }

return dp[PII(L, a)] = res;
        }

// reduce a
        ll ans = 0;
        ans += calc(L/2, reduce(a));

auto b = a;
        b.insert(b.begin(), a[0] ^ 1);
        ans += calc((L-1)/2, reduce(b));

return dp[PII(L, a)] = ans;
    };

ll ans = calc(L, a);
    printf("%lld\n", ans);
}
```

上一篇：数位dp（一）下一篇：区间dp在算法竞赛中的应用

看完文章有啥想法